One-N against the world!
We’re taking a short break from neural networks to return to portfolio optimization. Our last posts in the portfolio series discussed risk-constrained optimization. Before that we examined satisificing vs. mean-variance optimization (MVO). In our last post on that topic, we simulated 1,000 60-month (5-year) return series using the 1987-1991 period for our four assets: stocks, bonds, commodities (gold), and real estate. We then iterated through the samples using weights derived from the naive portfolio, the satisficing algorithm1, and the maximum Sharpe ratio portfolio on the previous sample to create portfolios on the next sample. We also randomly chose one portfolio, calculated the weights, and then randomly applied those weights on another portfolio.
We then examined performance across the weighting schemes. Interestingly, in both cases we found the naive and satisfactory portfolios outperformed the MVO-derived max Sharpe portfolio. These results echoed a paper that showed that various (complicated) versions of mean-variance optimization rarely performed better than the 1/N, or as we like to call it naive, portfolio. The 1/N is simply an equal-weighting of all assets in the portfolio; hence one over the number (N) of assets.
Of course, our post was nowhere near as sophisticated as three professors writing a scholarly article for equally scholarly peers. But they didn’t post their code in R or Python! We had shelved this research project until we started thinking about position sizing recently. In the real world, fundamental portfolio managers want to allocate capital to those assets they believe will have the greatest chance of producing the highest risk-adjusted returns. But what method should they use to estimate the ideal position size?
We’ve already discussed MVO and satisficing. But there are other methods too. The Kelly Criterion, popularized in books and blogs about legendary blackjack player and hedge fund manager Edward O. Thorp, tries to find optimal “bet” size. Others seek to lower estimation error—that is, the expected risk and/or return—or improve the optimization output to produce better out-of-sample performance.
MVO, as already shown, has its problems. We like our satisficing algorithm, but suspect it won’t catch on that soon. Ranking systems based on anticipated outperformance are reasonable, but may also be ad hoc. We haven’t experimented with the Kelly criterion or the other, more, sophisticated methods. All this got us thinking, what if we dusted off our portfolio series to test how the different optimization schemes would perform out-of-sample on real data?
Here’s how this will work. We’ll use the weighting schemes derived from historical data and then apply them to the next sequence of historical data. Typically, we’ll look at five-years of monthly data, run the algorithms, and then assign the weight output to the next five-years. As we roll forward in time, we’ll include the previous five years in the data set on which we run the algorithms. Since we start with the same dataset as before that will look like the following—train set 1: 1987-1991, test set 1: 1992-1996; train set 2: 1987-1996, test set 2: 1997-2001; and so on. Why five years? We’re long-term investors! Also, we don’t think the results of one-year forward returns are going to be that meaningful even if a year can seem like a lifetime when you’re managing money professionally. Nonetheless, if there’s interest, we’ll look at different sequence methods.
The optimization schemes we’ll be using are mean-variance optimization (MVO), as well as exponentially-weighted (12-month rolling) return estimates for MVO. We’ll also use a modified Kelly Criterion, the Black-Litterman model, and Hierarchical Risk Parity. We can’t really do justice to the last two methods. There are scores of papers describing them, but for a quick and dirty recap we recommend reading the docs of the PyPortfolioOpt package. We use a number of the classes and methods from this excellent package for this post, so have a look!
Let’s briefly discuss how the weighting schemes are derived. We’ll forego the naive discussion, as we expect most readers will get the 1/N weighting.
MVO and EW MVO
We’ve spilled enough pixelated ink to forego a lengthy discussion of the MVO portfolio algorithm. But suffice it to say, using convex optimization, one finds the weights that generate the maximum return for a given level of risk. The formula is:
max: μTw−γwTΣw
subject to: 1Tw=1
We won’t go into too much detail on the equation, as we’ve dealt with it before. While this is a general formula with γ representing a risk aversion metric, for this post we’ll actually be maximizing the Sharpe ratio or:
max: μTw(wTΣw)1/2
We’ll also use an exponentially-weighed version of returns to estimate future returns for the MVO.
Kelly criterion
Not usually used to find portfolio weights, the Kelly Criterion is discussed frequently by fundamental investors. Developed by John L. Kelly Jr. at Bell Labs to parse noise from signal, it found success at Vegas blackjack tables until the bosses figured it out, broke some knuckles, and added more decks to the dealer’s hand. The idea is to ask, how much should one “bet” as percent of his or her bankroll given an expected edge and desire never to go bankrupt. The elegantly simple formula is:
K%=w−1−wr
Where w is your expected win rate and r is the ratio of your win rate to loss rate. Note that if you’re expected win rate is 50%, the formula returns a 0 weight, or no bet. Smart formula.
We create an asset level Kelly, by deriving the win rate as the frequency of positive returns for the series. We calculate that for every asset and then scale the asset Kelly by the sum of all the asset Kellys to get a portfolio weight for each asset like the following:
Kelly weight: ki∑ni=1ki
We could get a little more sophisticated, but it’s been a long week.
Black-Litterman Model
Created by Fischer Black of Black-Scholes option pricing fame and Robert Litterman, the model seeks to improve on MVO. While it is impossible to do the model justice, think of it this way. The problem with MVO is that if you get your expected return estimate wrong you’re screwed. Mess up the estimates on your covariance matrix? That’s bad too, and there are a bunch of techniques to handle that. But bad return estimates tend to dominate the results2. Enter Black-Litterman, which tries to solve the return estimation problem by applying Bayesian methods3 to update one’s views on returns given the market price of risk.
Here’s the logic. Investors have views on returns. Probably not overly accurate views. But they’re more likely to be right about whether a set of assets will outperform another and which ones might enjoy higher excess returns. The model incorporates these views, by updating the market implied excess return base rate (the prior) with the forecasts modified by the confidence of that forecast, to return a new estimate of expected excess returns (the posterior). Here’s the formula.
E[R]=[(τΣ)−1+PTΩ−1P]−1[(τΣ)−1Π+PTΩ−1Q]
Don’t ask us to explain it! Essentially, it says expected returns (E[R]) are a function of prior market-implied expected returns (Π) and the investor’s views (Q) adjusted for uncertainty (Ω) on how much to weight (P) a particular asset. The covariance of the assets is also in there (Σ) along with another weighting mechanism (τ) that dictates the amount by which one should emphasize active vs. passive risk.4 Clear?
The important point about the BL model is that it’s not an optimization algorithm. It’s a way to get better return estimates to put into an MVO or other algorithm.
Hierarchical Risk Parity
This model is the brainchild of Marcos López de Prado, Cornell professor, Quant of the Year, and author of Advances in Financial Machine Learning. Again, very hard to encapsulate in a short paragraph. The main idea is to solve the portfolio allocation decision using machine learning instead of classical analytical techniques. At a basic level. Prado argues that MVO is unreliable because its leads to unstable solutions, asset concentrations that expose the portfolio to idiosyncratic risk, and out-of-sample underperformance. The reasons this occurs has to do with the math.5 But the intuition is when weights are unconstrained and without context, that can lead to substantially different solutions even when making small changes to the estimates. Prado solves this by introducing a hierarchical structure that prevents too much exposure to idiosyncratic risk.
Think of it this way. The traditional MVO solution would treat Exxon, Chevron, and ConocoPhillips as independent and might very well assign high weights to them in a high and rising oil environment. But a human PM would be worried about having too much energy exposure, especially when oil (inevitably) tanks. HRP is supposed to solve this, producing better diversification out-of-sample.6
Examining the models
So what do all these portfolio allocation algorithms look like? First, let’s visualize our starting point: the cumulative return graph of our four asset classes during the base period to run the algorithms: 1987-1991.
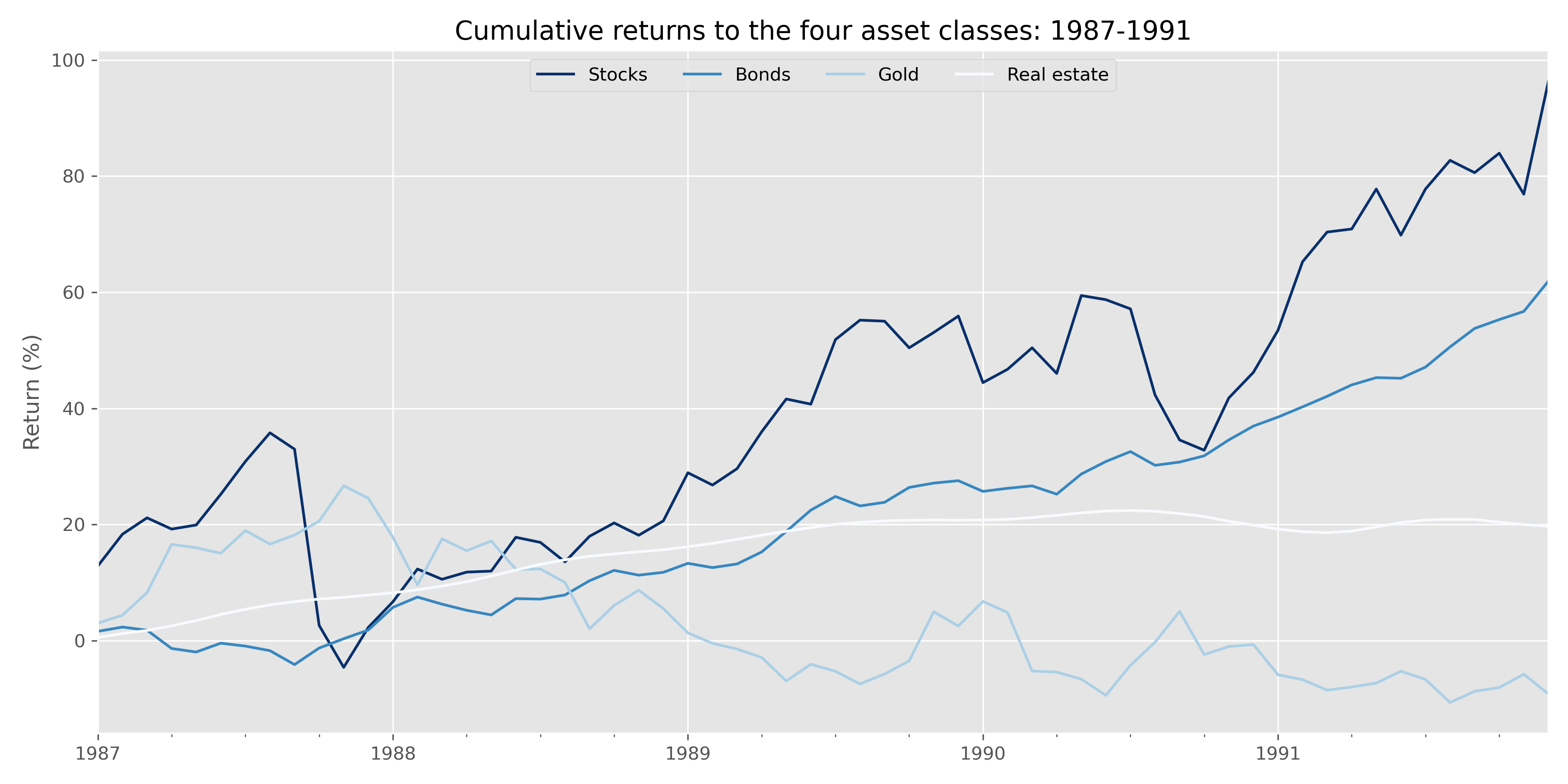
Stocks had a great run even if the ride was bit bumpy. Bonds weren’t bad either (Oh the days when bonds actually yielded something!). Real estate ticked along nicely, while the gold was a disappointment. Given these results, what weights would the various algorithms have recommended? Recall, for the MVO and BL portfolios, we’ve set the algorithm to pick the portfolio with the highest Sharpe ratio. The BL model requires us to input our view on expected returns and our confidence on those views, rather than interrupt the narrative, the reader can find these inputs after the code.
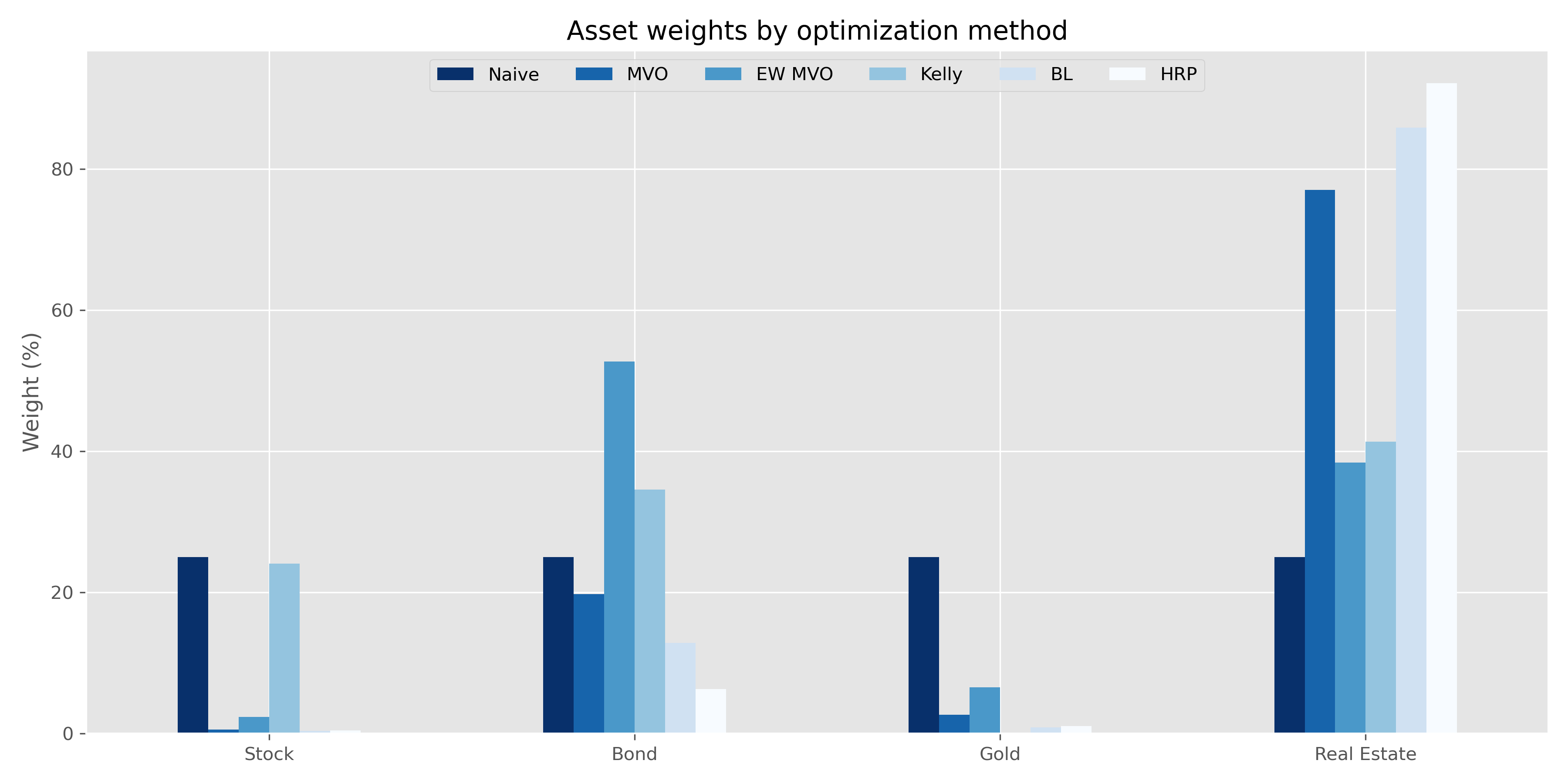
Interestingly, most of the portfolios select a high weighting to real estate. I don’t think any fundamental investor would have chosen the same weight. The Kelly portfolio seems to be the most reasonable. The exponentially-weighted MVO (EW MVO) features the lowest weighting to real estate after the naive portfolio. Although the weights on the naive portfolio should be obvious, we include them as reference.
Now let’s look at how these portfolios perform over the next period: 1992-1996. First, here’s the cumulative return graph.
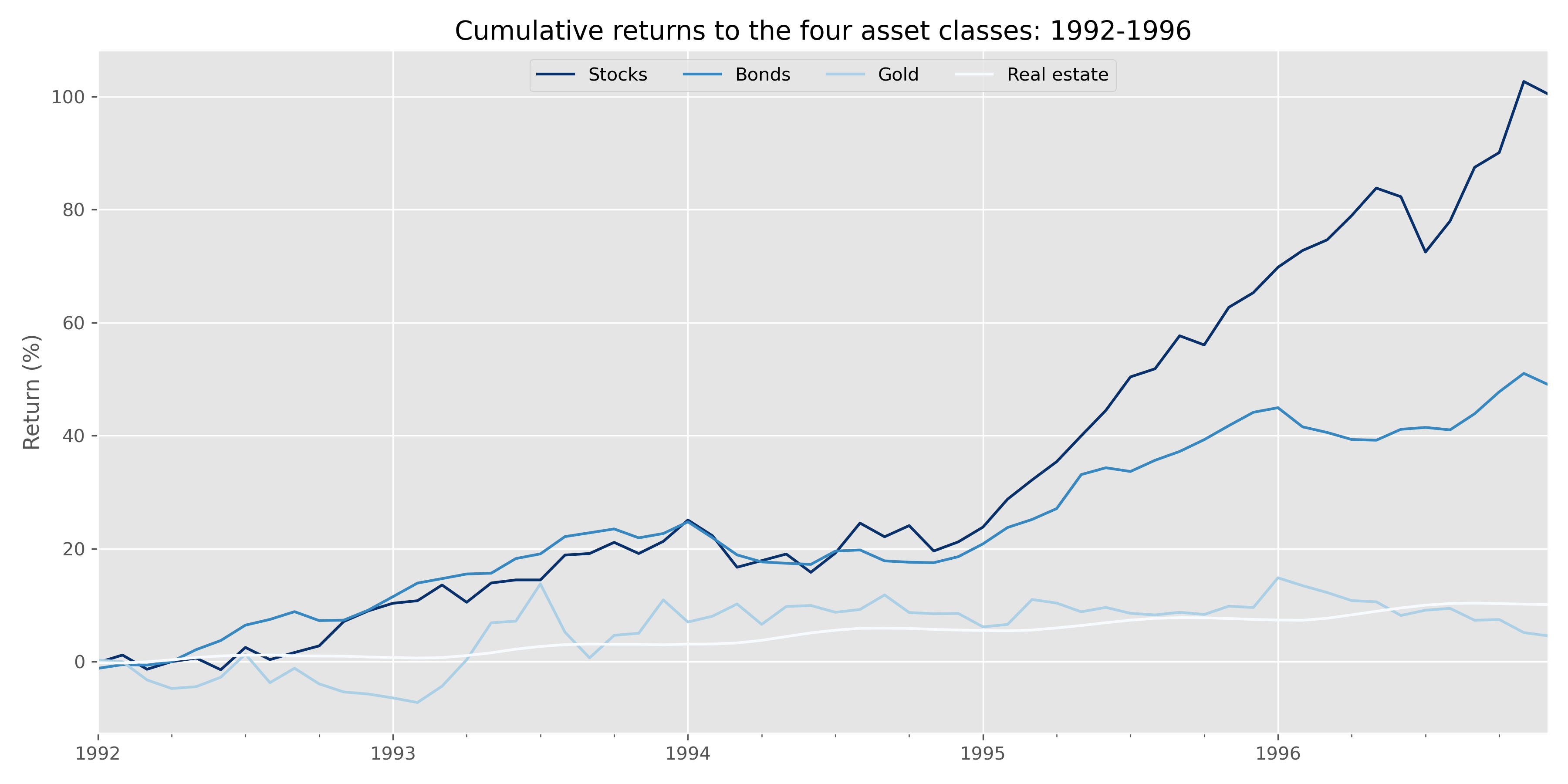
It should be relatively obvious that any portfolio that overweights the stock market relative to others will perform better. We show two versions of the weightings below. One with no rebalancing, the other with a yearly rebalance back to the original scheme. Note, that no rebalancing allows the weights to float, leaving the ending exposure often very different to the initial one.
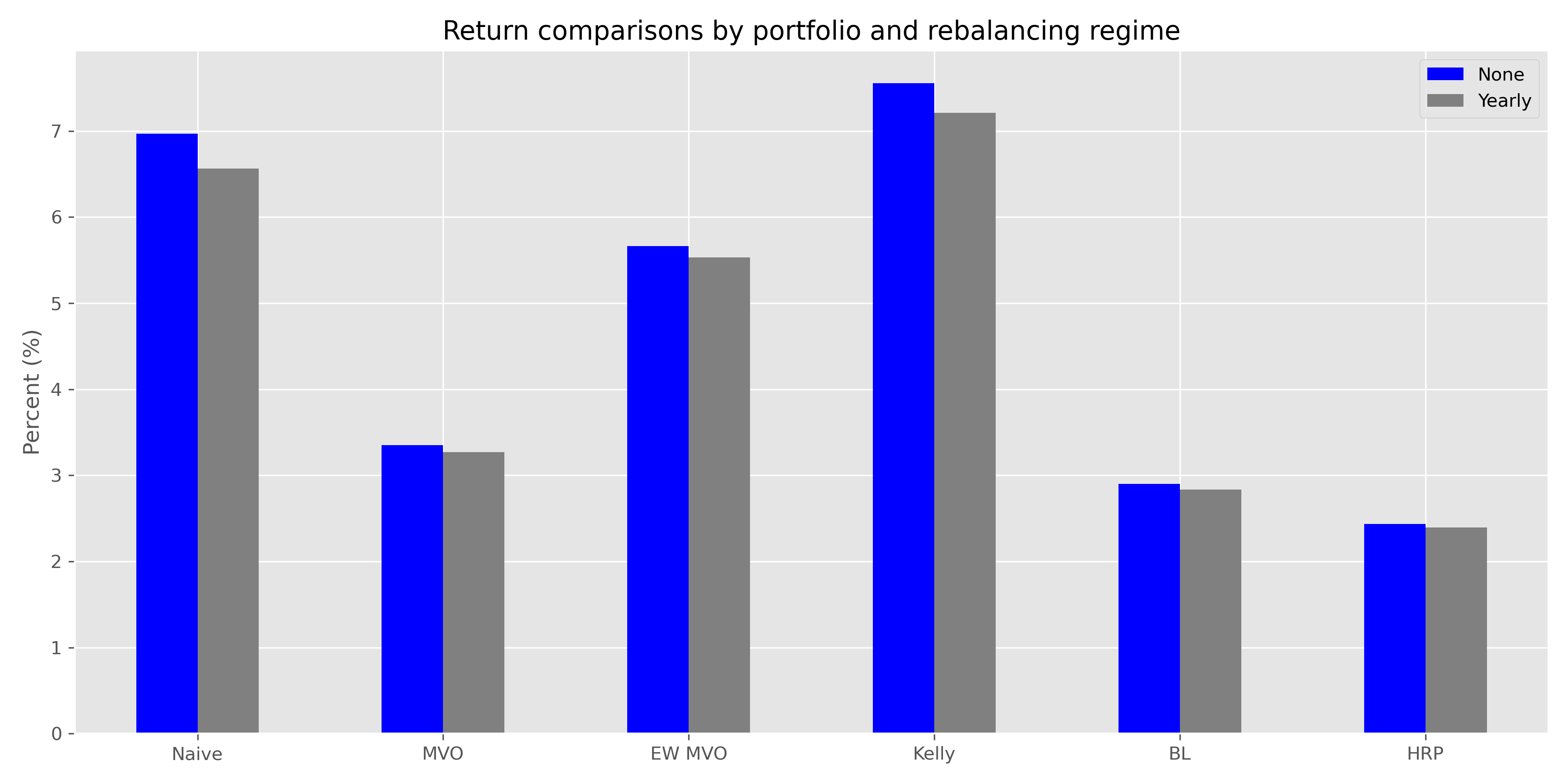
As is apparent, the Naive and Kelly portfolios outperform the more sophisticated algorithms given their higher exposure to stocks; though EW MVO wasn’t bad. We don’t think we need to run a t-test to prove that this outperformance was significant at around 400bps. One more thing to note is that yearly rebalancing underperformed no rebalancing. Something to consider especially if your robo-advisor advocates frequent rebalancing. Whatever the case, how did the portfolios perform in terms of the Sharpe ratio?
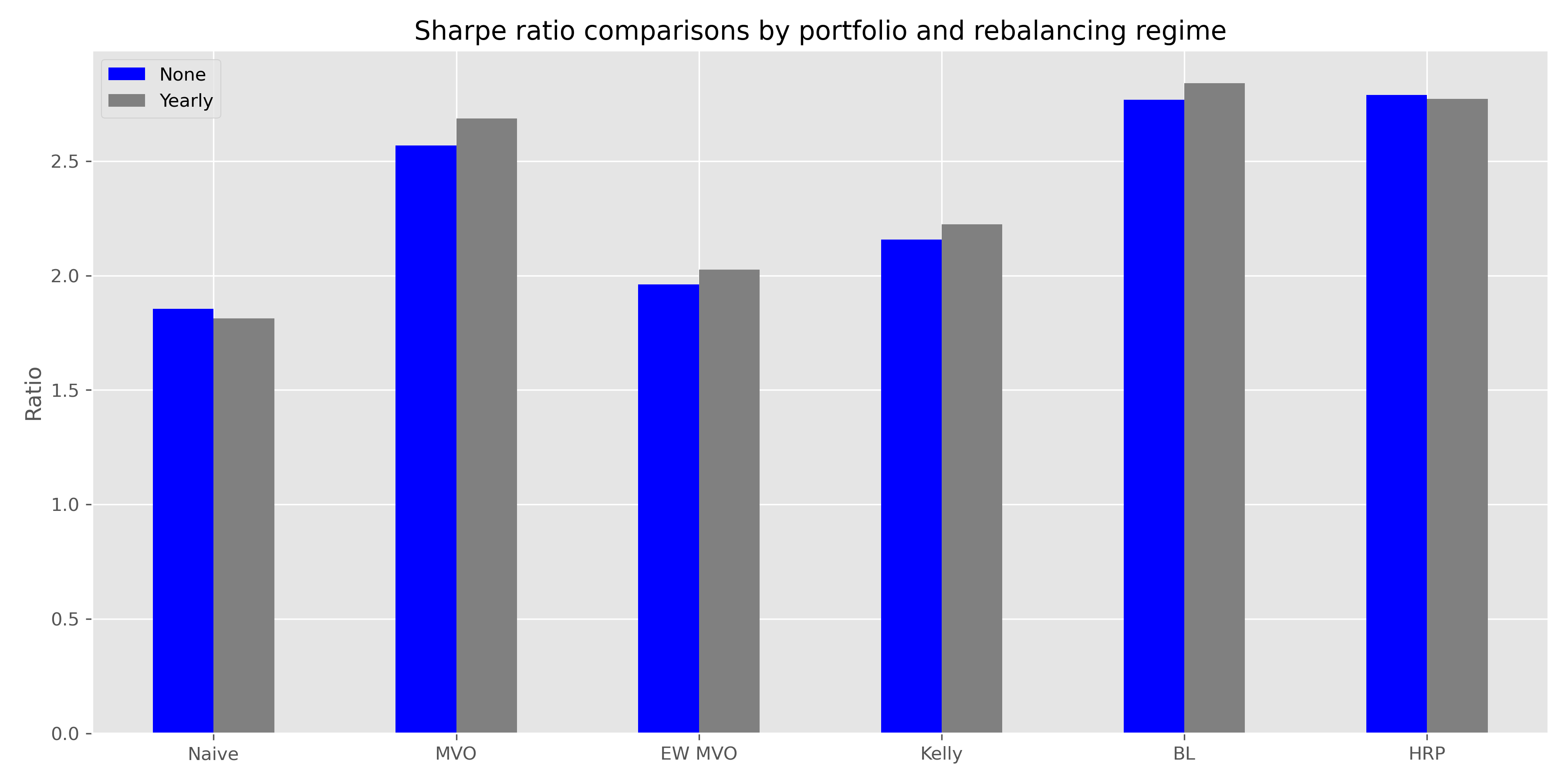
Not as well.7 The sophisticated algorithms clearly outperform the less sophisticated ones, except for EW MVO, which surprisingly performs worse than the Kelly portfolio. This sort of proves why you don’t want to rely too much on recent performance for your asset weightings.
Given the return outperformance and Sharpe underperformance of the simple weighting schemes relative to the sophisticated ones, it should be obvious that volatility is the main reason for the difference. We show the “vol” comparisons below.
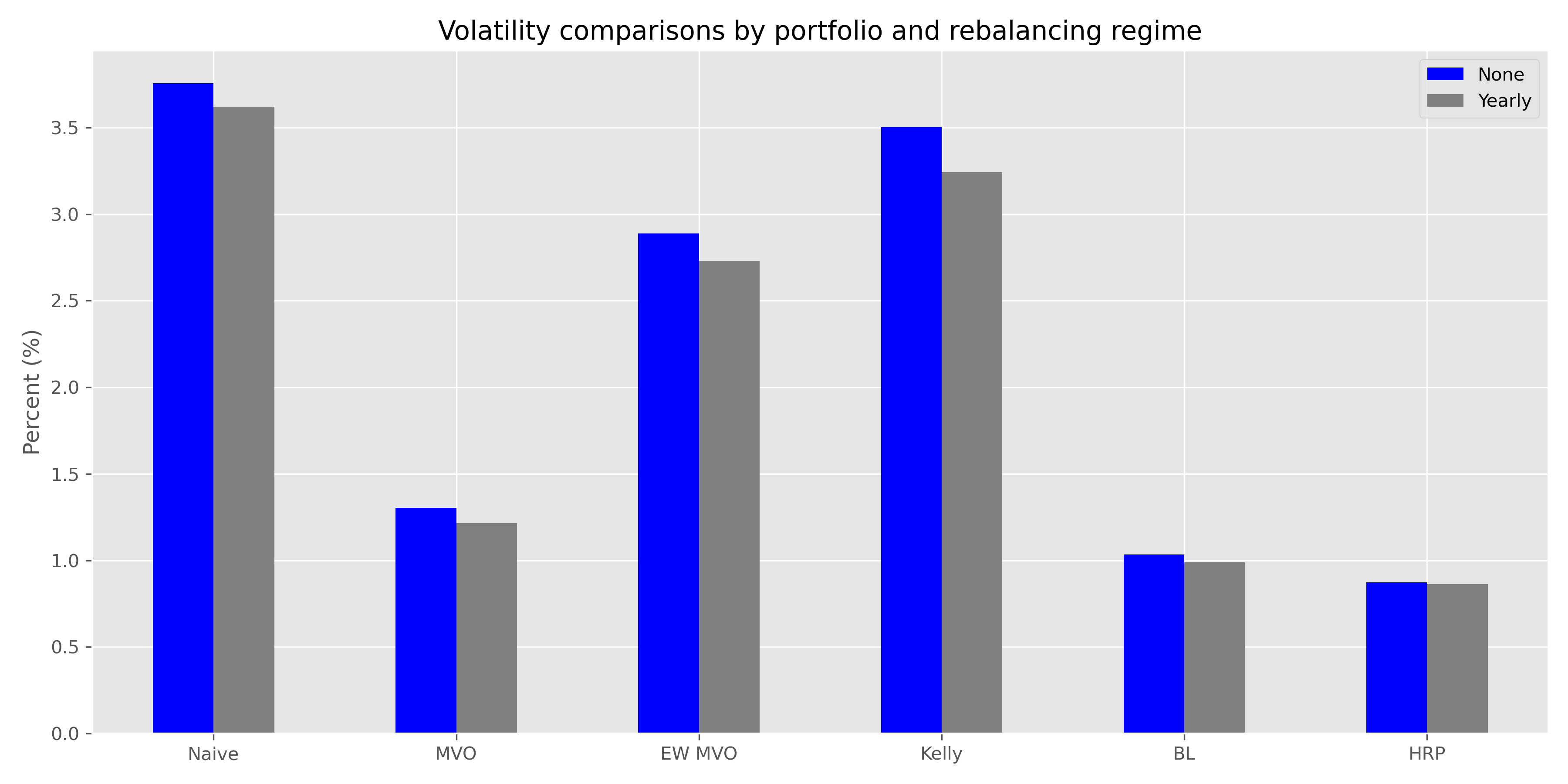
As they should, the algorithms meant to minimize risk for a given level of return, do exactly what they say on the tin. The simple algorithms clearly have significantly higher volatility on relative basis, but the overall base is quite low.
The key questions begged by these results are the following. Is it rational to suffer the slings and arrows of lower Sharpe ratios to enjoy a huge return advantage? Normative finance says no. But great investors say yes. Warren Buffett famously said he’d be happy with a volatile 15% return over a smooth 12% one.
Second, why did the Black-Litterman model and the Hierarchical Risk Parity perform similarly? They’re different approaches with different algorithms. This might be an artifact of the data or the expected return and conviction we used for the BL model. We suspect part of the reason is the paucity of assets. If there were more assets, the hierarchical algorithm would probably have differentiated itself as there would be, well, more hierarchies to distinguish between.
Third, is the Naive ratio, so naive after all? If we don’t really know the future, why not keep our asset weights on an even keel so we never miss the next wave? Why not minimize the probability of future regret as one Nobel Prize winner did?
We’ll end it here given that we’ve consumed more pixels than planned. In our next post, we’ll iterate through the other periods to get a total period performance of the different weighting schemes. If you have questions, you can reach us at the email address below. Until next time, here’s the code:
Built using R 4.0.3, and Python 3.8.8
[R]
## Load R libraries
suppressPackageStartupMessages({
library(tidyquant)
library(tidyverse)
library(reticulate)
})
# Apologies to R users. This post is all Python. If anyone knows of R library that approximates PyPortfolioOpt, please let us know!
[Python]
## Load packages
import pandas as pd
import pandas_datareader.data as dr
import numpy as np
import yfinance as yf
import pandas_datareader.famafrench as ffr
import cvxpy as cp
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12,6)
plt.style.use('ggplot')
## Save graphs for blog
import os
DIR = "C:/Users/user/path/to/blog/static"
def save_fig_blog(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(DIR, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
## Create dataset
start_date = '1970-01-01'
end_date = '2020-12-31'
symbols = ["WILL5000INDFC", "BAMLCC0A0CMTRIV", "GOLDPMGBD228NLBM", "CSUSHPINSA"]
sym_names = ["stock", "bond", "gold", "realt"]
filename = 'port_const_25.pkl'
try:
df = pd.read_pickle(filename)
print('Data loaded')
except FileNotFoundError:
print("File not found")
print("Loading data", 30*"-")
data = dr.DataReader(symbols, 'fred', start_date, end_date)
data.columns = sym_names
data_mon = data.resample('M').last()
dataf = data_mon.pct_change()
# Pull Fama-French risk-free rate. This series is different than what we find on FRED. We figure FF know what they're doing, so use their data!
ff_d = ffr.FamaFrenchReader('F-F_Research_Data_Factors_daily', start=start_date, end=end_date)
ff = ff_d.read()[0]
ff_mon = ff.resample('M').last()
df = pd.merge(dataf, ff_mon, how= 'left', left_index=True, right_index=True)
df.drop(['Mkt-RF','SMB','HML'], axis=1, inplace=True)
df.rename(columns= {'RF' : 'rfr'}, inplace=True)
df['rfr'] = new_df['rfr']/100
# Save for later use
df.loc['1987':].to_pickle('port_const_25.pkl')
## Create first series
df_1 = df.loc['1987':'1991', 'stock':'realt']
# Plot cumulative returns
(((1+df_1).cumprod()-1)*100).plot(cmap="Blues_r")
plt.xlabel("")
plt.ylabel("Return (%)")
plt.legend(['Stocks', 'Bonds', 'Gold', 'Real estate'], loc='upper center', ncol=4)
plt.title('Cumulative returns to the four asset classes: 1987-1991')
plt.show()
## MVO
# Function to return weights for maximum Sharpe ratio (tangency) portfolio
def max_sharpe(mu, sigma, samples=100):
w = cp.Variable(len(mu))
gamma = cp.Parameter(nonneg=True)
ret = mu.T @ w
risk = cp.quad_form(w, sigma)
objective = cp.Maximize(ret - gamma*risk)
prob = cp.Problem(objective, [cp.sum(w) == 1, w >= 0])
risk_data = np.zeros(samples)
ret_data = np.zeros(samples)
wt_data = np.zeros(samples, dtype=object)
gamma_vals = np.logspace(-2, 3, num=samples)
for i in range(samples):
gamma.value = gamma_vals[i]
prob.solve()
risk_data[i] = cp.sqrt(risk).value
ret_data[i] = ret.value
wt_data[i] = w.value
return wt_data[(ret_data/risk_data).argmax()]
# Run function
mu = df_1.mean().values # CVXPY needs numpy arrays
cov = df_1.cov().values
eff_sharpe = max_sharpe(mu, cov)
## EW MVO
mu_ema = df_1.ewm(12).mean().iloc[-1].values
ema_sharpe = max_sharpe(mu_ema, cov)
## Kelly Criterion
# Create function
def kelly(series):
win = sum(series > 0)/len(series)
loss = 1 - win
kelly = win - loss/(win/(loss+1e-6))
return 0 if kelly < 0 else kelly
# Run function
kelly_wts = df_1.apply(kelly)/df_1.apply(kelly).sum()
## Black-Litterman
from pypfopt import black_litterman, risk_models
from pypfopt import BlackLittermanModel, plotting
# Create function
# We're sorry we didn't go into more detail on how this works.
def get_bl_wts(return_data, mkt_cap_wt = np.array([0.12,0.48,0.5,0.35]),
views = {'stock':0.07, 'bond':0.05, 'gold':0.0, 'realt':0.04},
confidence = [0.75, 0.65, 0.5, 0.55]):
delta = (return_data.mean())/(return_data.var())
cov_mat = return_data.cov()
mkt_prior = delta * (cov_mat.values @ mkt_cap_wt)
bl = BlackLittermanModel(cov_mat, pi = mkt_prior,
absolute_views = views,
omega='idzorek',
view_confidences=confidence)
ret_bl = bl.bl_returns()
cov_bl = bl.bl_cov()
return max_sharpe(ret_bl.values, cov_bl.values)
## Hierarchical Risk Parity
from pypfopt import HRPOpt
def get_hrp_wts(return_data):
hrp = HRPOpt(return_data)
hrp.optimize()
return pd.Series(hrp.clean_weights())
## Graph weight comparisons
def wt_comp_plot(array, col_names = ['MVO', 'EW MVO', 'Kelly', 'BL'], ind_names = ['Stock', 'Bond', 'Gold', 'Real Estate'],
save_fig = False, png_name = None):
(pd.DataFrame(array*100,
columns = col_names,
index = ind_names)
.plot(kind='bar', cmap="Blues_r", rot=0))
plt.legend(loc='upper center', ncol=len(col_names))
plt.ylabel("Weight (%)")
plt.title("Asset weights by optimization method")
if save_fig:
save_fig_blog(png_name)
plt.show()
## Test the optimizations
# create test set
for_weights = np.c_[weights]
df_2 = df.loc['1992':'1996', 'stock':'realt']
rfr_2 = df.loc['1992':'1996', 'rfr']
# Create rebalancing function
def rebal_func(act_ret, weights, frequency=None):
"""Rebalancing logic:
If not rebalancing, as value of assets change, original weight in portfolio changes.
Need to adjust the weight for the overall return in the portfolio to calculate next period return.
Hence (weight_asset_i + return_asset_i) / (1 + return_portfolio).
If rebalancing, just multiply be original weight."""
beg_weights = weights
ret_vec = np.zeros(len(act_ret))
wt_mat = np.zeros((len(act_ret), len(act_ret.columns)))
for i in range(len(act_ret)):
if frequency:
if (i % frequency == 0) | (i < 1):
wt_ret = act_ret.iloc[i,:].values*beg_weights
else:
wt_ret = act_ret.iloc[i,:].values*new_weights
else:
if i < 1 :
wt_ret = act_ret.iloc[i,:].values*beg_weights
else:
wt_ret = act_ret.iloc[i,:].values*new_weights
ret = np.sum(wt_ret)
ret_vec[i] = ret
if frequency:
if (i % frequency == 0) | (i < 1):
new_weights = (beg_weights + wt_ret)/(1 + ret)
else:
new_weights = (new_weights + wt_ret)/(1 + ret)
else:
if i < 1 :
new_weights = (beg_weights + wt_ret)/(1 + ret)
else:
new_weights = (new_weights + wt_ret)/(1 + ret)
wt_mat[i,] = new_weights
return ret_vec, wt_mat
# Create function to port rebalancing results into data frame
def get_rebal_df(dataf, port_weights, ports=['Naive','MVO', 'EW MVO', 'Kelly', 'BL', 'HRP'], frequency = None):
if (port_weights.shape[1] != len(ports)) | (port_weights.shape[0] != len(dataf.columns)):
print("Weights and portfolios don't match!")
else:
results = {}
for i in range(len(ports)):
rets, wts = rebal_func(dataf, port_weights.T[i], frequency=frequency)
results[ports[i]] = {'returns':rets, 'weights': wts}
port_rets = []
for key in results.keys():
rets = results[key]['returns'].mean()*12
risk = results[key]['returns'].std()*np.sqrt(12)
sharpe = (rets)/risk
port_rets.append([rets, risk, sharpe])
return pd.DataFrame(port_rets, columns=['return', 'risk', 'sharpe'], index = ports)
port_df = get_rebal_df(df_2, for_weights)
port_rebal_df = get_rebal_df(df_2, for_weights, frequency=12)
# Create function plot results
def port_comp_plot(dataf1, metric, dataf2 = None, ports = ['Naive','MVO', 'EW MVO', 'Kelly', 'BL', 'HRP'],
save_fig=False, png_name=None):
if dataf2 is not None:
(pd.DataFrame(np.c_[dataf1[metric], dataf2[metric]],
columns = ['None', 'Yearly'],
index = ports)
.plot(kind='bar', color=['blue', 'grey'], rot=0))
else:
(pd.DataFrame(np.c_[dataf1[metric]],
index = ports)
.plot(kind='bar', color='blue', rot=0, legend=None))
metric_dict = {'return':'Return', 'sharpe':'Sharpe ratio', 'risk': 'Volatility'}
metric_label = {'return':'Percent (%)', 'sharpe':'Ratio', 'risk': 'Percent (%)'}
plt.ylabel(metric_label[metric])
if dataf2 is not None:
plt.title("{} comparisons by portfolio and rebalancing regime".format(metric_dict[metric]))
else:
plt.title("{} comparisons by portfolio".format(metric_dict[metric]))
if save_fig:
save_fig_blog(png_name)
plt.show()
# Plot results: returns, Sharpe ratio, volatility
port_comp_plot(port_df*100, 'return', port_rebal_df*100)
port_comp_plot(port_df, 'sharpe', port_rebal_df)
port_comp_plot(port_df*100, 'risk', port_rebal_df*100)Black-Litterman inputs
As noted above, the Black-Litterman model requires the user to input his or her expected returns for various assets as well as the conviction around those expectations. We arbitrarily chose those inputs below. A more thoughtful approach might take long-term historical returns and assign a 70% probability to that. The difficulty is figuring out what the average investor or portfolio manager thought future returns were going to be in 1991. Could someone lend us a time machine?
| Asset | Return | Conviction |
|---|---|---|
| Stock | 7.0 | 75.0 |
| Bond | 5.0 | 65.0 |
| Gold | 0.0 | 50.0 |
| Real estate | 4.0 | 55.0 |
Essentially, simulating three thousand different weighting schemes across the four assets and taking average of the weights that achieved the desired risk/return profile.↩︎
Returns scale by time, volatility scales by the square root of time↩︎
P(A|B)=P(B|A)P(A)P(B)↩︎
Nonetheless, the function of τ still leaves a lot of folks scratching their heads.↩︎
According to Prado, the issue is that “quadratic optimizers require the inversion of the covariance matrix.” Sounds hard. We’ll take his word for it!↩︎
While we haven’t done the analysis, it seems like one could limit sector exposure by constraining sector weights within the MVO framework. Whether that would produce the same results out-of-sample as HRP is for another time.↩︎
Note how amazing the Sharpe ratios look. Part of this is that volatility on monthly returns once annualized is usually a bit less than annualized daily volatility, making the Sharpe ratios look much better.↩︎