Day 18: Autocorrelation Again!
On Day 17 , we compared the 12-by-12 and 200-day SMA strategies in terms of magnitude and duration of drawdowns, finding in favor of the 200-day. We also noted that most of the contributors to the differences in performance were due to two periods at the beginning and end of the period we were examining. That suggests regime driven performance, which begs the question, how much can we rely on our analysis if we have no certainty that any of the regimes identified will recur, or, even be forecastable?! What’s a quant analyst to do?
Simulate future performance. This is something that Marcos Lopez de Prado discusses frequently in Advances in Financial Machine Learning and it is indeed a broad topic that is impossible to cover in a short blog post. Nonetheless, we can sketch the idea and offer up some code for readers to test. As discussed, a backtest gives us a snapshot of historical performance. But we want to quantify the likelihood of success of a strategy going forward. What to do? Simulate possible paths and use the aggregate results to construct an expected performance estimate. How do you simulate? One way is to sample from a distribution that approximates the distribution of returns found in the strategy. A second way is sampling from history. A third way is to mix and match or add another distribution to approximate the uncertainty and randomness of the future.
There are problems with all of these. For the first way, most financial returns don’t follow standard distributions found in statistics. We can approximate a distribution using a Gaussian Mixture Model, but we still don’t know if the future distribution will look like this. For the second way, naive sampling of past returns can give you close to the same answer as you already calculated in the backtest.1 For the third way, this is interesting and we don’t have a method to recommend, but it could be a little ad hoc. Indeed, statistics is pretty good at modeling random variables. The struggle we have is we’re trying to model uncertain ones. We don’t know which random variable distribution the future will draw from!
Whatever the case, we’ve rambled on a bit, so let’s get to the data. While the historical simulation method has problems, we prefer it insofar as it is approachable and explainable. The key is to account explicitly for the autocorrelation of returns. Instead of sampling individual returns, we sample blocks of returns and concatenate them to create a synthetic, but modestly realistic series. The key is figuring out the size of the block. Back to autocorrelation plots!
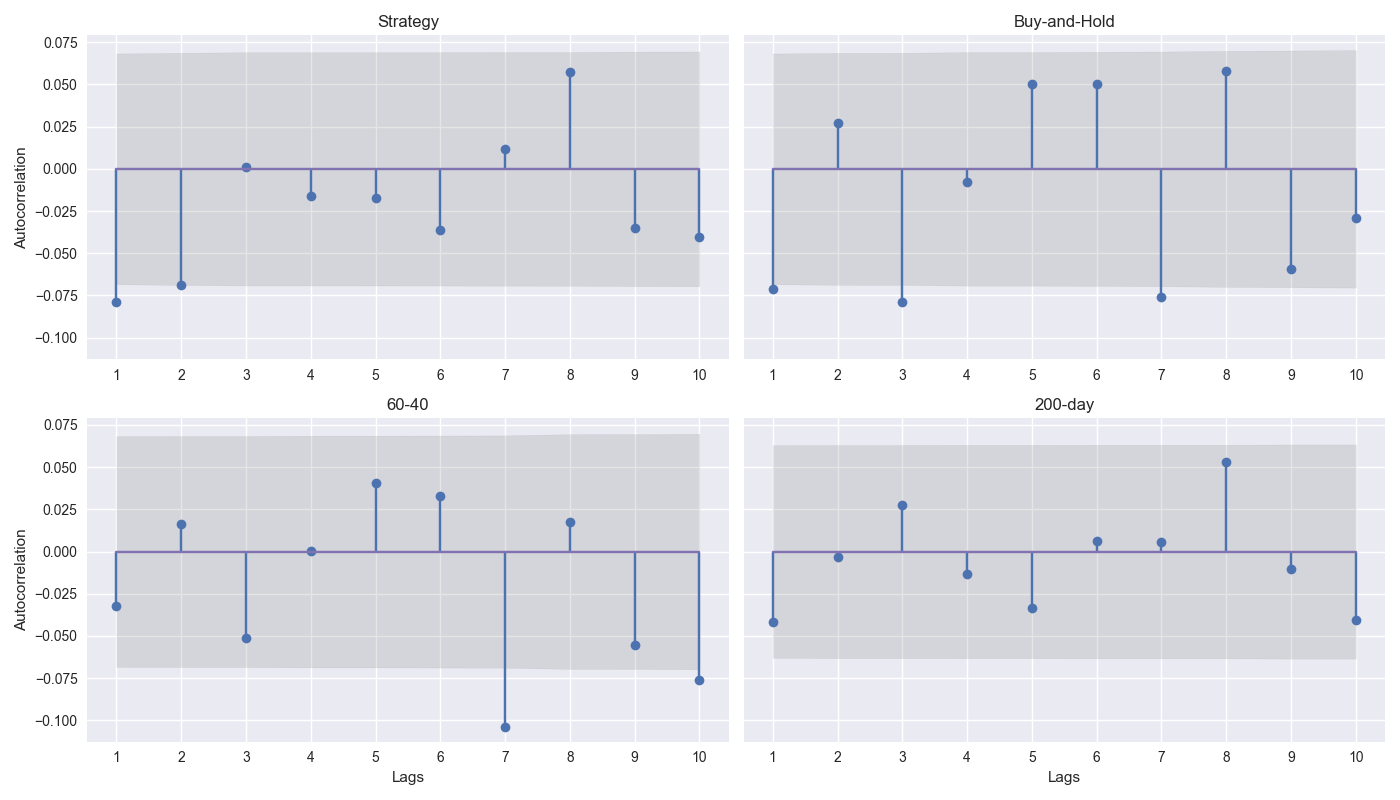
In the graph below, we show four autocorrelation plots for the strategy with the three benchmarks as a first step to identifying a reasonable basis for block size. In the graphs, we show the correlation for the 1-to-10 week lag as well as a shaded area for the confidence interval. Dots that fall out of that shaded area are significant autocorrelation lags. We’ll discuss these results in more detail in our next post. Code below.
# Built using Python 3.10.19 and a virtual environment
# Load libraries
import pandas as pd
import numpy as np
from datetime import datetime, timedelta
import statsmodels.api as sm
import matplotlib.pyplot as plt
import yfinance as yf
from matplotlib.ticker import FuncFormatter
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import acf
plt.style.use('seaborn-v0_8')
plt.rcParams['figure.figsize'] = (14,8)
# Function to get data
def get_spy_weekly_data() -> pd.DataFrame:
df = yf.download('SPY', start='2000-01-01', end='2024-10-01')
df.columns = ['open', 'high', 'low', 'close', 'adj close', 'volume']
df.index.name = 'date'
# Create training set and downsample to weekly ending Friday
df_train = df.loc[:'2019-01-01', 'adj close'].copy()
df_w = pd.DataFrame(df_train.resample('W-FRI').last())
df_w.columns = ['price']
return df_w
# Get data
df_w = get_spy_weekly_data()
# Create momentum dictionary
periods = [3, 6, 9, 12]
momo_dict = {}
for back in periods:
for forward in periods:
df_out = df_w.copy()
df_out['ret_back'] = np.log(df_out['price']/df_out['price'].shift(back))
df_out['ret_for'] = np.log(df_out['price'].shift(-forward)/df_out['price'])
df_out = df_out.dropna()
mod = sm.OLS(df_out['ret_for'], sm.add_constant(df_out['ret_back'])).fit()
momo_dict[f"{back} - {forward}"] = {'data': df_out,
'params': mod.params,
'pvalues': mod.pvalues}
# Prepare model
model_name = '12 - 12'
mod_look_forward = 12
train_pd = 5
test_pd = 1
tot_pd = train_pd + test_pd
# Create trading dataframe
df_trade = momo_dict[model_name]['data'].copy()
# Run model with train/forecast steps
trade_pred = []
for i in range(tot_pd, len(df_trade)+1, test_pd):
train_df = df_trade.iloc[i-tot_pd:i-test_pd, 1:]
test_df = df_trade.iloc[i-test_pd+mod_look_forward-1:i-test_pd+mod_look_forward, 1:]
# Ensure 'ret_back' is 2D by selecting it as a DataFrame, not a Series
X_train = sm.add_constant(train_df[['ret_back']])
if test_df.shape[0] > 1:
X_test = sm.add_constant(test_df[['ret_back']])
else:
X_test = sm.add_constant(test_df[['ret_back']], has_constant='add')
# Fit the model
mod_run = sm.OLS(train_df['ret_for'], X_train).fit()
# Predict using the test data
mod_pred = mod_run.predict(X_test).values
trade_pred.extend(mod_pred)
# Test for length
assert len(trade_pred) + mod_look_forward + train_pd - 1 == len(df_trade)
# Add predictions to dataframe
df_trade['pred'] = np.concatenate((np.repeat(np.nan, mod_look_forward + train_pd - 1), np.array(trade_pred)))
# Generate returns
df_trade['ret'] = np.log(df_trade['price']/df_trade['price'].shift(1))
# Generate signals
df_trade['signal'] = np.where(df_trade['pred'] == np.nan, np.nan, np.where(df_trade['pred'] > 0, 1, 0))
df_trade['signal_sh'] = np.where(df_trade['pred'] == np.nan, np.nan, np.where(df_trade['pred'] >= 0, 1, -1))
# Generate strategy returns
df_trade['strat_ret'] = df_trade['signal'].shift(1) * df_trade['ret']
df_trade['strat_ret_sh'] = df_trade['signal_sh'].shift(1) * df_trade['ret']
# Load data for 60-40
data = yf.download(['SPY', 'IEF'], start='2000-01-01', end='2024-10-01')
df = data.loc["2003-01-01":, 'Adj Close']
df.columns.name = None
tickers = ['ief', 'spy']
df.index.name = 'date'
df.columns = tickers
df[['ief_chg', 'spy_chg']] = df[['ief','spy']].apply(lambda x: np.log(x/x.shift(1)))
df_bw = pd.DataFrame(df.resample('W-FRI').last())
df_bw[['ief_chg', 'spy_chg']] = df_bw[['ief','spy']].apply(lambda x: np.log(x/x.shift(1)))
# Align dates for comparisons
end_date_bench = df_trade.index[-1].strftime("%Y-%m-%d")
bench_returns = df_bw[['ief_chg', 'spy_chg']].copy()
bench_returns = bench_returns.loc[:end_date_bench]
bench_returns = bench_returns.dropna()
strat_returns_start = bench_returns.index[0].strftime("%Y-%m-%d")
strat_returns = df_trade['strat_ret'].copy()
strat_returns = strat_returns.loc[strat_returns_start:]
# Create function to calculate portfolio performance
def calculate_portfolio_performance(weights: list, returns: pd.DataFrame, rebalance=False, frequency='month') -> pd.Series:
# Initialize the portfolio value to 0.0
portfolio_value = 0.0
portfolio_values = []
# Initialize the current weights
current_weights = np.array(weights)
# Create a dictionary to map frequency to the appropriate offset property
frequency_map = {
'week': 'week',
'month': 'month',
'quarter': 'quarter'
}
if rebalance:
# Iterate over each row in the returns DataFrame
for date, daily_returns in returns.iterrows():
# Apply the current weights to the daily returns
portfolio_value = np.dot(current_weights, daily_returns)
portfolio_values.append(portfolio_value)
# Rebalance at the selected frequency (week, month, quarter)
offset = pd.DateOffset(days=1)
next_date = date + offset #type: ignore
# Dynamically get the attribute based on frequency
current_period = getattr(date, frequency_map[frequency])
next_period = getattr(next_date, frequency_map[frequency])
# If current period does not equal next period, time to rebalance
if current_period != next_period:
current_weights = np.array(weights)
else:
# Update weights based on the previous day's returns
current_weights = current_weights * (1 + daily_returns)
current_weights /= np.sum(current_weights)
else:
# No rebalancing, just apply the initial weights
for date, daily_returns in returns.iterrows():
portfolio_value = np.dot(current_weights, daily_returns)
portfolio_values.append(portfolio_value)
# Update weights based on the previous day's returns
current_weights = current_weights * (1 + daily_returns)
current_weights /= np.sum(current_weights)
daily_returns = pd.Series(portfolio_values, index=returns.index)
return daily_returns
# Create 60-40 portfolio
weights = [0.4,0.6]
bench_60_40_rebal = calculate_portfolio_performance(weights, bench_returns, rebalance=False, frequency='quarter')
bench_60_40_rebal.index = bench_60_40_rebal.index.tz_localize(None) #type:ignore
# Create 200-day strategy
df_200 = df_w.copy()
df_200.columns = ['price']
df_200 = df_200.resample('W-FRI').last()
# 40 weeks = 200 days
df_200['sma_200'] = df_200['price'].rolling(40).mean()
df_200['ret'] = np.log(df_200['price']/df_200['price'].shift(1))
df_200['signal'] = np.where(df_200['price'] > df_200['sma_200'], 1, 0)
df_200['strat_ret'] = df_200['signal'].shift(1)*df_200['ret']
df_200_bench = df_200.loc[df_trade['strat_ret'].index[0]:df_trade['strat_ret'].index[-1]]
# Plot ACF
return_data = [strat_returns, bench_returns['spy_chg'], bench_60_40_rebal, df_200_bench['strat_ret']]
names = ['Strategy', 'Buy-and-Hold', '60-40', '200-day']
fig, axs = plt.subplots(2, 2, sharey=True)
for idx, (data, name) in enumerate(zip(return_data, names)):
# Calculate the autocorrelation
acf_values, confint = acf(data.dropna(), nlags=10, alpha=0.05) #type: ignore
lower_bound = confint[1:, 0] - acf_values[1:]
upper_bound = confint[1:, 1] - acf_values[1:]
# Find the correct subplot (axs[0, 0], axs[0, 1], etc.)
ax = axs[idx // 2, idx % 2]
ax.stem(range(1, len(acf_values)), acf_values[1:])
# Set x-ticks to match lag numbers
ax.set_xticks(range(1, len(acf_values)))
ax.set_xticklabels(range(1, len(acf_values)))
# Add shaded area for confidence interval
ax.fill_between(range(1, len(acf_values)), upper_bound, lower_bound, color='gray', alpha=0.2)
ax.set_title(name)
if idx > 1:
ax.set_xlabel("Lags")
if idx % 2 == 0:
ax.set_ylabel("Autocorrelation")
plt.tight_layout()
plt.show()Think of it this way. Were we to sample with replacement from the same jellybean urn 1000s of times, we’d ultimately approach the average value of the urn that we would have found if we had simply dumped all the jellybeans out and counted the color before eating them and subsequently getting a belly ache.↩︎