Not so soft softmax
Our last post examined the correspondence between a logistic regression and a simple neural network using a sigmoid activation function. The downside with such models is that they only produce binary outcomes. While we argued (not very forcefully) that if investing is about assessing the probability of achieving an attractive risk-adjusted return, then it makes sense to model investment decisions as probability functions. Moreover, most practitioners would probably prefer to know whether next month’s return is likely to be positive and how confident they should be in that prediction. They want to get direction right first. That’s binary.
But what about magnitude and relative performance? Enter multiclass logistic regression and neural networks with the softmax activation function. Typically multiclass (or multinomial) classifications are used to distinguish categories like Pekingese from Poodles, or Shih-tzus. With a bit of bucketing, one can do the same with continuous variables like stock returns. This may reduce noise somewhat, but also gets at the heart of investing: the shape of returns. Most folks who’ve been around the markets for a while know that returns are not normally distributed, particularly for stocks.1 Sure, they’re fat-tailed and often negatively skewed. Discussed less frequently is that these returns also cluster around the mean. In other words, there are far more days of utter boredom, sheer terror, or unbearable ecstasy2 than implied by the normal distribution.
While everyone wants to knock the ball out of the park and avoid the landmines, those events are difficult to forecast given their rarity even for the fat-tailed distribution. Sustained performance is likely to come from compounding in the solid, but hardly heroic area above the mean return near the one sigma boundary. These events are more frequent and also offer more data with which to work. Indeed, since 1970 almost 40% of the S&P 500’s daily returns fell into that area vs. the expectation of only 34% based on the normal distribution.
How would be go about classifying the probability of different returns? First, we’d bucket the returns according to some quantile and then run the regression or neural network on those buckets to get the predictions. Multiclass logistic regressions use the softmax function which looks like the following:
\[ Softmax(k, x_{1}, ..,, x_{n}): \Large\frac{e^{x_{k}}}{\sum_{i=1}^{n}e^{x_{i}}} \]
\[ f(k) = \begin{cases} 1 \text{ if } k = argmax(x_{1},...,x_{n}) \\ 0 \text{ othewise} \end{cases} \]
Here \(x_{k}\) is whatever combination of weights and biases with the independent variable that yields the maximum value for a particular class. Thus that value over the sum of all the exponentiated values yields the model’s likelihood for a particular category. How exactly does this happen? A multiclass logistic regression aggregates individual logistic regressions for the probability of each category with respect to all the other categories. Then it uses the fact that the probabilities must sum to one to yield the softmax function above. The intuition is relatively straightforward: how often do we see one class vs. all the rest based on some data? Check out the appendix for a (slightly!) more rigorous explanation.
Let’s get to our data, split it into the four quartiles for simplicity and then run a logistic regression on those categories. Recall we’re using the monthly return on the S&P500 as well as the return on the 10-month moving average vs. the one-month forward return, which we transform into the four buckets: below -1.9%, between -1.9% and 0.5%, between 0.5% and 3.6%, and above 3.6%. We’ll dub these returns with the following technical terms: Stinky, Poor, Mediocre, Good
Now we’ll run the regressions and present the confusion matrix as before.
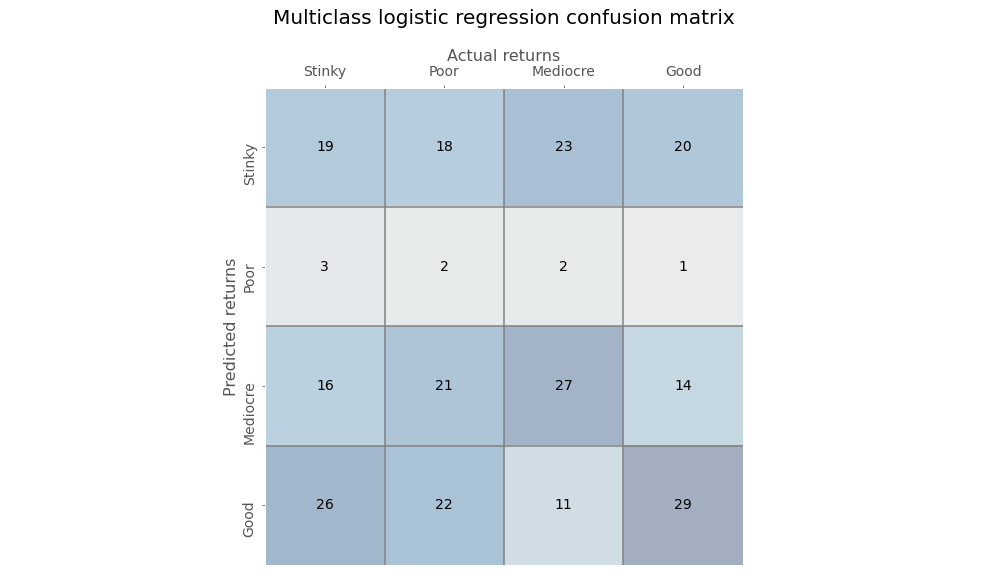
Whoa dude, is this some weird sudoku? Not really. Still, a four-by-four confusion matrix isn’t the easiest to read. Bear with us as we explain. The diagonal from the upper left to the lower right contains the true positives. The rows associated with each true positive are the false positives while the columns are the false negatives. The true negative is essentially all the other cells that don’t appear in either the row or the column for the particular category. So the true negative for the Stinky category would be the sum of the 3x3 matrix whose top left corner starts in the cell of the second row and second column.
Organizing the data this way is better than nothing, but it could be more insight provoking. We can see that the multiclass logistic regression is not that strong in the Poor category, but is much better in the Good category. Let’s compute the true positive and false positive rates along with the precision for each category, which we show in the table below.
| Outcome | TPR | FPR | Precision |
|---|---|---|---|
| Stinky | 29.7 | 32.1 | 23.7 |
| Poor | 3.2 | 3.1 | 25.0 |
| Mediocre | 42.9 | 26.7 | 34.6 |
| Good | 45.3 | 31.1 | 33.0 |
Even with the refinement this still isn’t the easiest table to interpret. The model’s best true positive rate (TPR) performance is in the Good category, but it’s false positive rate (FPR) is also one of the highest. Shouldn’t we care about being really wrong? True, we don’t want to be consistently wrong. But we really don’t want to believe we’re going to generate a really good return and end up with a really Stinky one.
We’ll create a metric called the Really Wrong Rate (RWR) which will be the number of really wrong classifications over the total classifications the model made for that category. For example, for the Stinky outcome, the model got 19 correct (the top left box) but got 20 really wrong (the top right box). Thus its RWR is about 25% and its Precision to RWR is about 0.95. In other words, it’s getting more categories really wrong than correct.
What about the others? For the Good category, its RWR rate is almost 30% and its Precision to RWR is 1.12. That seems like a good edge. The model is really right about 12% more than it’s really wrong. However, when if you look at correctly identified categories plus incorrectly identified positive returns (the Good and Mediocre columns) relative to incorrectly identified categories with negative returns (the Stinky and Poor columns), the results are much worse: a ratio of about 0.83. Got that? Let’s move on to the neural network, before we get bogged down in confusion matrix navel gazing.
Unlike the linear regression or binary logistic regression, a simple neural network can’t approximate a multiclass logistic regression easily. Indeed, it takes a bit of wrangling to get something close, so we won’t bore you with all the iterations. We will show one or two just so you know how much effort we put in!
First, a single layer perceptron, with four output neurons, and a softmax activation function. We graph the model’s accuracy over 100 epochs along with logistic regression accuracy—the red dotted line—below.
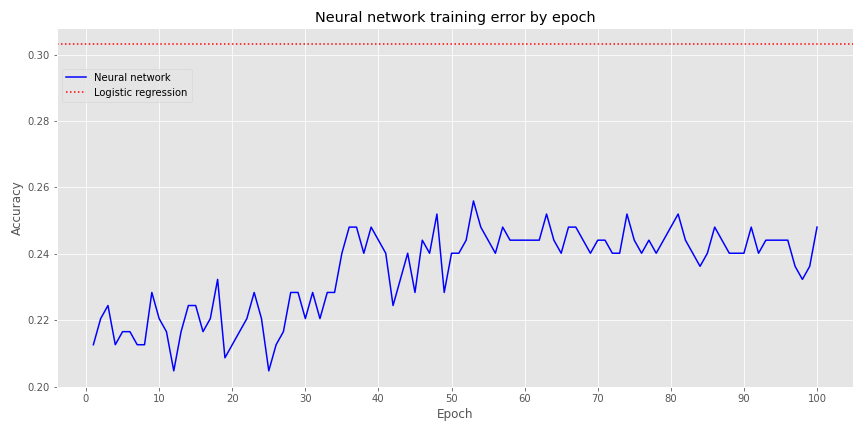
Not very inspiring. When we include a hidden layer with 20 neurons (an entirely arbitrary number!), but the same parameters as before, we get the following graph.
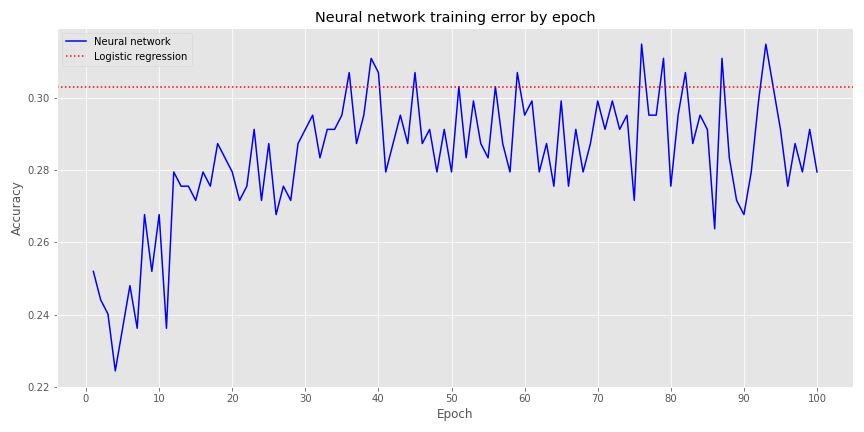
Definitely better. We see that around the 37th epoch, the NN’s accuracy converges with the logistic regression, but it does bounce around above and below that for the remaining epochs.
Let’s build a deeper NN, this time with three layers of 20 neurons each. For graphical purposes, the architecture of this NN looks like the following:
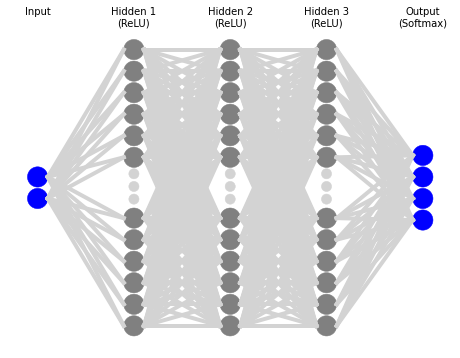
Plotting accuracy by epoch, gives us the next graph:
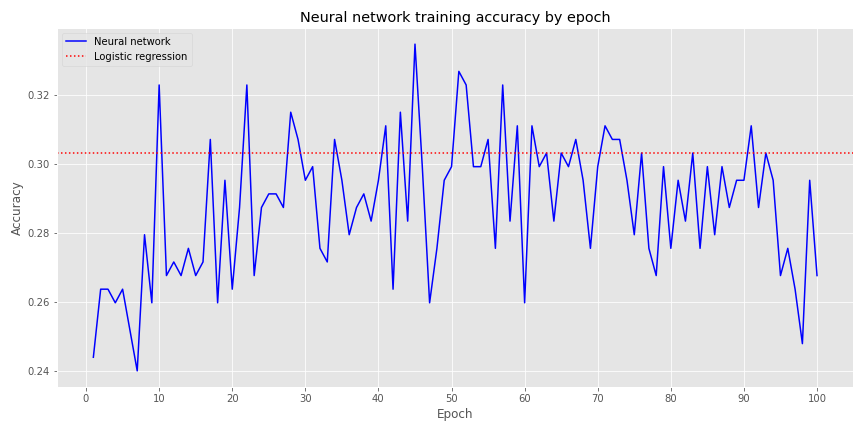
This denser NN achieves a better accuracy than the logistic regression sooner than the others, and it’s outperformance persists longer. Of course, even when it does perform worse, it isn’t that dramatic—about one or two percentage points.
We’ll stop the model at the first point that it converges with the logistic regression, which happens to the be the tenth epoch and create the confusion matrix is below.
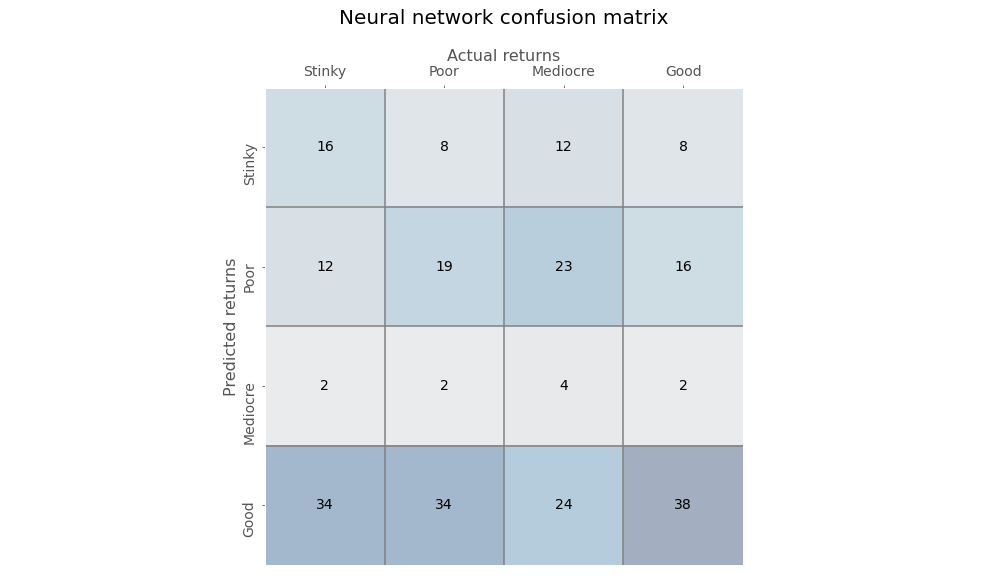
Again, a bit of struggle to discern much from this table, other than the model does not appear to predict Mediocre returns with much frequency even though they represent about 25% of the occurrences. Let’s look at some of the scores.
| Outcome | TPR | FPR | Precision |
|---|---|---|---|
| Stinky | 25.0 | 14.7 | 36.4 |
| Poor | 30.2 | 26.7 | 27.1 |
| Mediocre | 6.3 | 3.1 | 40.0 |
| Good | 59.4 | 48.4 | 29.2 |
The NN model has a much better true positive rate (TPR) than the logistic regression for Good outcomes, but the false positive rate (FPR) is high too. While the NN model is worse than the regression model on Stinky outcomes, it’s FPR is less than half that of the regression. Interestingly, both models are poor at predicting one category: Poor outcomes for the regression model vs. Mediocre outcomes for the NN. We’re not sure why that would be the case.
The Stinky RWR is about 18% yielding a Precision to RWR ratio of 2 on the Stinky outcomes, much better than the logistic regressions ratio of 0.95. In other words, the NN is twice as likely to predict a Stinky outcome correctly than incorrectly predict a Good outcome as a Stinky one.
Should we favor the logistic regression over a NN with softmax activation? Hard to say. Accuracy results are similar, but we did have to play with the NN a lot more. More than accuracy, once you look under the hood, results diverge. The greater flexibility of the NN might help us tune a model to arrive at our desired true positive, false positive, and or really wrong rates. But that might come at the risk of overfitting. Moreover, it’s still unclear why both models picked one category as less likely even though the each category should have had an equal chance of occurring. We’d need to engage in more data analysis to figure out what we’re missing.
What are some other avenues we could explore? We could build denser neural networks. We could backtest the predictions to gauge performance. This would probably be done best using walk-forward analysis. Of course, a drawback with this is that few people were using neural networks to run trading algorithms during the 70s and 80s so the results could be spurious. That is, if people had been employing such algorithms, returns could have been a lot different. Another avenue is to change the bucketing mechanism so that we focus on the range of outcomes we’re most interested in or would be most likely to achieve high risk-adjusted returns.
We’ll leave those musings for now. Let us know what you’d like to read by sending an email to the address below. Want more on multiclass regressions and softmax functions? Or should we explore if neural networks can approximate decision trees and random forests? Let us know! Until then, have a look at the Appendix after the code. It walks through the link between logistic and softmax functions. And by all means, have a look at the code!
Built using R 4.0.3, and Python 3.8.3
# [R]
# Load libraries
suppressPackageStartupMessages({
library(tidyverse)
library(tidyquant)
library(reticulate)
})
# [Python]
# Load libraries
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib
import matplotlib.pyplot as plt
import os
os.environ['QT_QPA_PLATFORM_PLUGIN_PATH'] = 'C:/Users/user_name/Anaconda3/Library/plugins/platforms'
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (12,6)
# Directory to save images
DIR = "your/image/directory"
def save_fig_blog(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(DIR, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dip=resolution)
## Pull data and split
# See past posts for code
sp_mon = pd.read_pickle('sp_mon_tf_2.pkl')
data = sp_mon.dropna()
X_train = data.loc[:'1991', ['ret', '10ma_ret']]
y_train = data.loc[:'1991', '1_mon_ret']
X_valid = data.loc['1991':'2000', ['ret', '10ma_ret']]
y_valid = data.loc['1991':'2000', '1_mon_ret']
X_test = data.loc['2001':, ['ret', '10ma_ret']]
y_test = data.loc['2001':, '1_mon_ret']
y_train_trans = pd.qcut(y_train, 4, labels=[0, 1, 2, 3])
# Modest search for best solvers and regularization hyperparameters
from sklearn.linear_model import LogisticRegression
solvers = ['lbfgs', 'newton-cg', 'sag', 'saga']
for solver in solvers:
log_reg = LogisticRegression(penalty='l2', solver = solver, multi_class='multinomial')
log_reg.fit(X_train, y_train_trans)
log_pred = log_reg.predict(X_train)
print(log_reg.score(X_train, y_train_trans))
Cs = [10.0**-x for x in np.arange(-2,3)]
for c in Cs:
log_reg = LogisticRegression(penalty='l2', multi_class='multinomial', C=c)
log_reg.fit(X_train, y_train_trans)
print(log_reg.score(X_train, y_train_trans))
log_reg = LogisticRegression(penalty='l2', multi_class='multinomial')
log_reg.fit(X_train, y_train_trans)
log_reg.score(X_train, y_train_trans)
## Sigmoid on four classes
# Not shown
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
y_train_cat = keras.utils.to_categorical(y_train_trans)
model = keras.models.Sequential([
keras.layers.Dense(4, activation='sigmoid',input_shape = X_train.shape[1:])
])
model.compile(loss='binary_crossentropy', optimizer='sgd', metrics=['accuracy'])
history = model.fit(X_train, y_train_cat, epochs = 100)
## Softmax on four clases
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(4, activation='softmax')
])
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
history = model.fit(X_train, y_train_cat, epochs=100)
# Graph accuracy
log_score = log_reg.score(X_train, y_train_trans)
log_hist_df = pd.DataFrame(history.history)
log_hist_df.index = np.arange(1, len(log_hist_df)+1)
log_hist_df['accuracy'].plot(style='b-')
plt.axhline(log_score, color='red', ls = ':')
plt.xticks(np.arange(0,len(log_hist_df)+1, 10))
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title("Neural network training error by epoch")
plt.legend(['Neural network', 'Logistic regression'], loc='upper left', bbox_to_anchor=(0.0, 0.9))
save_fig_blog('nn_vs_log_reg_tf3')
plt.show()
## Softmax with one hidden layer
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(20, activation='relu', input_shape=X_train.shape[1:]),
keras.layers.Dense(4, activation='softmax')
])
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
history = model.fit(X_train, y_train_cat, epochs=100)
# Graph
log_score = log_reg.score(X_train, y_train_trans)
log_hist_df = pd.DataFrame(history.history)
log_hist_df.index = np.arange(1, len(log_hist_df)+1)
log_hist_df['accuracy'].plot(style='b-')
plt.axhline(log_score, color='red', ls = ':')
plt.xticks(np.arange(0,len(log_hist_df)+1, 10))
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title("Neural network training error by epoch")
plt.legend(['Neural network', 'Logistic regression'], loc='upper left')
save_fig_blog('nn_vs_log_reg_2_tf3')
plt.show()
## Three hidden layer architecture
from nnv import NNV
layersList = [
{"title":"Input\n", "units": 2, "color": "blue"},
{"title":"Hidden 1\n(ReLU)", "units": 20},
{"title":"Hidden 2\n(ReLU)", "units": 20},
{"title":"Hidden 3\n(ReLU)", "units": 20},
{"title":"Output\n(Softmax)", "units": 4,"color": "blue"},
]
NNV(layersList,max_num_nodes_visible=12, node_radius=8, font_size=10).render(save_to_file=DIR+"/nn_tf3.png")
plt.show()
## Softmax with three hidden layers
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential()
model.add(keras.layers.Dense(20, activation='relu', input_shape=X_train.shape[1:]))
for layer in range(2):
model.add(keras.layers.Dense(20, activation='relu'))
model.add(keras.layers.Dense(4, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
history = model.fit(X_train, y_train_cat, epochs=100)
log_score = log_reg.score(X_train, y_train_trans)
log_hist_df = pd.DataFrame(history.history)
log_hist_df.index = np.arange(1, len(log_hist_df)+1)
log_hist_df['accuracy'].plot(style='b-')
plt.axhline(log_score, color='red', ls = ':')
plt.xticks(np.arange(0,len(log_hist_df)+1, 10))
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title("Neural network training accuracy by epoch")
plt.legend(['Neural network', 'Logistic regression'], loc='upper left')
save_fig_blog('nn_vs_log_reg_3_tf3')
plt.show()
## Rerun stopping early
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential()
model.add(keras.layers.Dense(20, activation='relu', input_shape=X_train.shape[1:]))
for layer in range(2):
model.add(keras.layers.Dense(20, activation='relu'))
model.add(keras.layers.Dense(4, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
history = model.fit(X_train, y_train_cat, epochs=10)
## Create confusion matrix table function
# Help from SO
# https://stackoverflow.com/questions/50666091/true-positive-rate-and-false-positive-rate-tpr-fpr-for-multi-class-data-in-py/50671617
from sklearn.metrics import confusion_matrix
# from sklearn.metrics import precision_score, recall_score, roc_curve
def conf_mat_table(predicted, actual, title = 'Logistic regression', save=False, save_title = None, print_metrics=False):
conf_mat = confusion_matrix(y_true=predicted, y_pred=actual)
fig, ax = plt.subplots(figsize=(14,8))
ax.matshow(conf_mat, cmap=plt.cm.Blues, alpha=0.3)
for i in range(conf_mat.shape[0]):
for j in range(conf_mat.shape[1]):
ax.text(x=j, y=i, s=conf_mat[i, j], fontsize=14, va='center', ha='center')
ax.xaxis.set_ticks_position('top')
ax.xaxis.set_label_position('top')
ax.set_xticklabels(['','Stinky', 'Poor','Mediocre', 'Good'], fontsize=14)
ax.set_yticklabels(['', 'Stinky', 'Poor', 'Mediocre', 'Good'], fontsize=14, rotation=90)
ax.set_xlabel('Actual returns', fontsize=16)
ax.set_ylabel('Predicted returns', fontsize=16)
ax.tick_params(axis='both', which='major', pad=5)
ax.set_title(title + ' confusion matrix', pad=40, fontsize=20)
lines = [0.5, 1.5, 2.5]
for line in lines:
plt.axhline(line, color='grey')
plt.axvline(line, color='grey')
plt.grid(False)
if save:
save_fig_blog(save_title)
plt.show()
if print_metrics:
FP = conf_mat.sum(axis=1) - np.diag(conf_mat)
FN = conf_mat.sum(axis=0) - np.diag(conf_mat)
TP = np.diag(conf_mat)
TN = conf_mat.sum() - (FP + FN + TP)
# Add 1e-10 to prevent division by zero
# True positive rate
tpr = TP/(TP+FN+1e-10)
# Precision
precision = TP/(TP+FP+1e-10)
# False positive rate
fpr = FP/(FP+TN+1e-10)
print("")
tab = pd.DataFrame(np.c_[['Stinky', 'Poor','Mediocre', 'Good'], tpr, fpr, precision],
columns = ['Outcome', 'TPR', 'FPR', 'Precision']).set_index("Outcome")
tab = tab.apply(pd.to_numeric)
return tab, conf_mat
## Predictions
log_pred = log_reg.predict(X_train)
nn = model.predict(X_train)
nn_pred = np.argmax(nn, axis=1)
## Logistic regression table
tab1, conf_mat1 = conf_mat_table(log_pred, y_train_trans, save=False, title="Multiclass logistic regression",
print_metrics=True, save_title='log_reg_conf_mat_1_tf3')
# Save to csv for blog
dir1 = "your/wd"
folder = "/your_folder/"
tab1.to_csv(dir1+folder+'tab1_tf3.csv')
conf_mat1 = pd.DataFrame(data = conf_mat1, index=pd.Series(['Stinky', 'Poor','Mediocre', 'Good'], name='Outcome'),
columns=['Stinky', 'Poor','Mediocre', 'Good'])
conf_mat1.to_csv(dir1+folder+'/conf_mat1_tf3.csv')
# [R]
# Rmarkdown table
# Asssumes we're in the directory to which we saved all those csvs.
tab1 <- read_csv('tab1_tf3.csv')
tab1 %>%
mutate_at(vars("TPR", "FPR", "Precision"),
function(x) format(round(x,3)*100,nsmallest=0)) %>%
knitr::kable(caption = "Logistic regression scores (%)")
conf_mat1 <- read_csv('conf_mat1_tf3.csv')
stinky_rwr <- as.numeric(conf_mat1[1,5]/sum(conf_mat1[1,2:5]))
good_rwr <- as.numeric(conf_mat1[4,2]/sum(conf_mat1[4,2:5]))
stinky_prec <- as.numeric(tab1[1,4])
good_prec <- as.numeric(tab1[4,4])
good_2_Stinky <- (sum(conf_mat1[4,4:5])/sum(conf_mat1[4,2:3]))
# [Python]
## Neutral network table
tab2, conf_mat2 = conf_mat_table(nn_pred, y_train_trans, title="Neural network", save=False, print_metrics=True, save_title='nn_conf_mat_1_tf3')
# Save to csv for blog
tab2.to_csv(dir1+folder+'/tab2_tf3.csv')
conf_mat2 = pd.DataFrame(data = conf_mat2, index=pd.Series(['Stinky', 'Poor','Mediocre', 'Good'], name='Outcome'),
columns=['Stinky', 'Poor','Mediocre', 'Good'])
conf_mat2.to_csv(dir1[:-13]+'/conf_mat2_tf3.csv')
conf_mat2.to_csv(dir1+folder+'/conf_mat2_tf3.csv')
# [R]
# Rmarkdown table
# Neural network
# Asssumes we're in the directory to which we saved all those csvs.
tab2 <- read_csv('tab2_tf3.csv')
tab2 %>%
mutate_at(vars("TPR", "FPR", "Precision"), function(x) format(round(x,3)*100,nsmallest=0)) %>%
knitr::kable(caption = "Neural network scores")
conf_mat2 <- read_csv('conf_mat2_tf3.csv')
stinky_rwr1 <- as.numeric(conf_mat2[1,5]/sum(conf_mat2[1,2:5]))
good_rwr1 <- as.numeric(conf_mat2[4,2]/sum(conf_mat2[4,2:5]))
stinky_prec1 <- as.numeric(tab2[1,4])
good_prec1 <- as.numeric(tab2[4,4])
good_2_Stinky1 <- (sum(conf_mat2[4,4:5])/sum(conf_mat2[4,2:3]))Appendix3
While we think the intuition behind the softmax function is relatively straightforward, deriving it is another matter. Our search has revealed simplistic discussions or mathematical derivations that require either a lot of formulas with matrix notation or several formulas and a hand wave. While our aim is not to write tutorials, we do think it can be helpful to provide more rigor on complex topics. In general, we find most of the information out there on the main ML algorithms either math-averse or math-enchanted. There’s got to be a happy medium: one that gives you enough math to understand the nuances in a more formal way, but not so much that you need to have aced partial differential equations without ever having taken ordinary ones.4 Here’s our stab at this.
Let’s refresh our memories on softmax and logistic functions:
\[ Softmax(k, x_{1}, ..,, x_{n}): \Large\frac{e^{x_{k}}}{\sum_{i=1}^{n}e^{x_{i}}} \]
\[ f(k) = \begin{cases} 1 \text{ if } k = argmax(x_{1},...,x_{n}) \\ 0 \text{ othewise} \end{cases} \] \[ \\ Logisitic: \Large\frac{e^{x}}{1 + e^{x}} \\ \]
The logic behind the softmax function is as follows. Suppose you have a bunch of data that you think might predict various classes or categories of something of interest. For example, tail, ear, and snout length for a range of different dog breeds. First you encode the labels (e.g., breeds) as categorical variables (essentially integers). Then you build a neural network and apply weights and biases to the features (e.g. tail, etc). You then compare the output of the neural network against each label. But you need to transform the outputs into something that will tell you that a tail, ear, and snout of lengths x, y, and z are more likely to belong to a Poodle than a Pekingese. All you’ll get from applying weights and biases to all the features are bunches of numbers with lots of decimal places. You need some way to “squash” the data into a probabilistic range to say which breed is more likely that another given an input. Enter the softmax function.
Look at the formula and forget Euler’s constant (\(e\)) for a second. If you can do that, you should be able to see the softmax function as a simple frequency calculation: the number of Shih-tzus over the total number of Shih-tzus, Pekingese, and Poodles in the data set. Now recall that we’re actually dealing with lots of weights and biases applied to the variables, which could have different orders of magnitude once we’re finished with all the calculations. By raising Euler’s constant to the power of the final output, we set all values to an equivalent base, and we force the largest output to be much further away from all the others, unless there’s a tie. This has the effect of pushing the model to chose one class more than all the others.5 Not so soft after all! Once we’ve transformed the outputs, we can them compare each one to the sum of the total to get the probability for each breed. The output with the highest probability that corresponds one of the breeds means that the model believes it’s that particular breed. We can then check against the actual breed, calculate a loss function, backpropagate, and rerun.
But how does this relate to the logistic function other than that both use \(e\)?
If perform some algebra on the logistic function we get:6
\(\Large e^{x} = \frac{y}{1-y}\)
Thus \(e^{x}\) is the probability of some outcome over the probability of not that outcome. Hence, each \(e^{x}\) is equivalent to saying here’s the probability this a Pekingese vs. Not a Pekingese given the features. If we recognize that Not a Pekingese is essentially all other breeds, then we can see how to get to the numerator in the softmax function. To transform this into a probability distribution in which all probabilities must sum to one, we sum all the \(e^{x}\)s. That’s the softmax denominator: \(\sum_{i=1}^{n}e^{x_{i}}\).
Whew! For such a rough explanation that was pretty long-winded. Can we try to derive the softmax function from the logistic function mathematically? One of the easiest ways is to reverse it using a two case scenario.
If we only have Pekingese (\(e^{x_{p}}\)) and Shih-tzus (\(e^{x_{s}}\)), then the probability for each is:
\(\Large e^{x_{p}} = \frac{p}{1-p} = \frac{p}{s}\)
\(\Large e^{x_{s}} = \frac{s}{1-s} = \frac{s}{p}\)
Where:
\(x_{p}, x_{s}\) are the different weighted features that yield a Pekingese or a Shih-tzu
\(p, s\) are the probability of being a Pekingese or a Shih-tzu
Thus if we’re trying to estimate the probability of a Pekingese, the simplified calculation using the softmax function looks like the following?
\(\Large\frac{e^{x_{p}}}{e^{x_{p}} + e^{x_{s}}}\)
If the evidence for the Shih-tzu is zero, that means \(x_{s}\) is zero and hence \(e^{x_{s}}\) is \(1\). Which resolves to:
\(\Large\frac{e^{x_{p}}}{1 + e^{x_{p}}}\)
The logistic function! Neat, but doesn’t this seem like a sleight of hand? It’s not as obvious how it would work if we were to add a third category like a Poodle. Moreover, it doesn’t exactly help us build the softmax function from the logistic.
If we start with the log-odds as we did in the last post, that might prove to be more fruitful. Recall for a binary outcome it looks like the following:
\(\Large log(\frac{p_{i}}{1-p_{i}}) = \beta_{i} x\)
Let \(p_{i}\) be the probability of one class
And let \(Z = (1 - p_{i})\) represent all the other possible classes\
\(\beta_{i} x\) represents the particular weights applied to x to arrive at \(p_{i}\).
Then,
\(\Large p_{i} = \frac{e^{\beta_{i} x}}{Z}\)
Since all the probabilities must sum to 1:
\(\Large 1 = \sum \frac{e^{\beta_{i}x}}{Z}\)
Since Z is a constant, it can be pulled out of the summation:
\(\Large 1 = \frac{1}{Z} \sum e^{\beta_{i}x}\)
This yields:
\(\Large Z = \sum e^{\beta_{i}x}\)
Thus:
\(\Large p_{i} = \frac{e^{\beta_{i}x}}{\sum_{i=i}^{K} e^{\beta_{i}x}}\)
Magic! The softmax function.
We’ve been meaning to do a post comparing return distributions between asset classes, but haven’t got around to it. If you’ve seen a good article on the subject, please email us at the address below. We don’t want to reinvent the wheel!↩︎
We actually heard this phrase on the Streetwise podcast recently and thought it was too funny to pass up.↩︎
When we first started to write this section we thought we could encapsulate it pretty easily. Instead, we had a hard time pulling ourselves out of the rabbit hole. If something seems wrong or off, let us know!↩︎
Like my lovely wife!↩︎
This doesn’t always work and sometimes features need to be normalized prior to training or need an additional ‘jiggering’ at activation. We don’t know about you, but even though we get the logic behind using exponentiation, we can’t help but wonder whether it is biasing results just for force a more emphatic outcome. If you can shed light on this for us, please email us at the address below.↩︎