Testing expectations
In our last post, we analyzed the performance of our portfolio, built using the historical average method to set return expectations. We calculated return and risk contributions and examined changes in allocation weights due to asset performance. We briefly considered whether such changes warranted rebalancing and what impact rebalancing might have on longer term portfolio returns given the drag from taxes. At the end, we asked what performance expectations we should have had to analyze results in the first place. It’s all well and good to say that a portfolio performed by “X”, but shouldn’t we have had a hypothesis as to how we expected the portfolio to perform?
Indeed we did. As we noted in the post, the historical averages method assumes the future will resemble of the past. But that is a rather nebulous statement. It begs the question, by how much? In this post, we aim to develop a framework to quantify the likelihood our portfolio will meet our expected performance targets. This approach is very much influenced by a talk given by Prof. Marcos López de Prado. Among the many things discussed, the one that struck us most is the role simulation plays vis a vis backtesing. True, simulation has it’s own issues, but at least you’re not relying on a single trial to formulate a hypothesis. Basing an investment strategy on the results of what happened historically is, in many ways, basing it on a single trial no matter how much one believes history repeats, rhymes, or rinses.
Enough tongue-wagging, let’s get to the data! Here’s our road map.
- Review the data
- Simulate possible return outcomes
- Incorporate portfolio weighting simulation
- Summarize and critique the simulations
- Next steps
Review data
Recall, our portfolio was comprised of the major asset classes: stocks, bonds, commodities (gold), and real estate. Data was pulled from the FRED database and began in 1987, the earliest date for a complete data set.
We took the average return and risk of those assets for the period of 1987 to 1991 and constructed 1,000 portfolios based on random weights. We then found all the portfolios that met our criteria of not less than a 7% return and not more than 10% risk on an annual basis. The average weights of those selected portfolios became our portfolio allocation for the test period. We calculated the return and risk for our portfolio (without rebalancing) during the first test period and compared that within another simulation of 1,000 possible portfolios. We graph that comparison below.
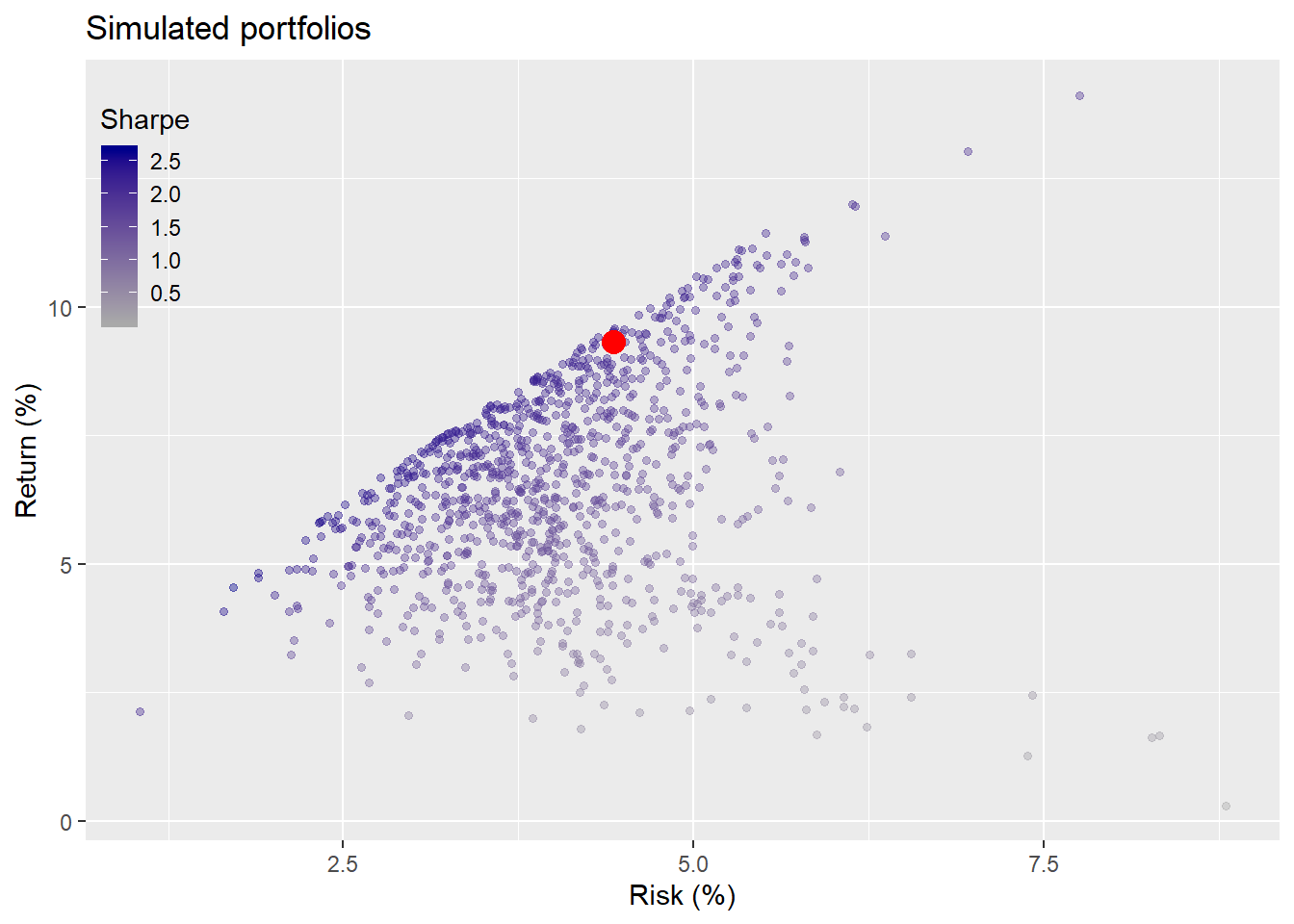
First simulation
If you’re thinking, why are we talking about more simulations when we’ve already done two rounds of them, it’s a legitimate question. The answer: we didn’t simulate potential returns and risk. Remember we took the historical five-year average return and risk of the assets and plugged those numbers into our weighting algorithm to simulate potential portfolios. We didn’t simulate the range of potential returns. It should be obvious that the returns we hoped to achieve based on our portfolio allocation were not likely to be the returns we would achieve. But what should we expect? Only 27% of the portfolios in our simulation would have achieved our risk-return constraints based on using the historical average as a proxy for our return expectation.
Is that an accurate probability? Hard to tell when we’re basing those return expectations on only one period. A more scientific way of looking at it could be to run a bunch of simulations to quantify how likely the risk and return constraints we chose would occur.
We’ll simulate 1,000 different return profiles of the four asset classes using their historical average return and risk. But instead of only using data from 1987, the earliest date in which we have a full data set, we’ll calculate the average based on as much of the data as is available. That does create another bias, but in this case only relates to real estate, which has the shortest period from our data source.
Before we proceed, we want to flag a problem with simulations: your assumptions around risk and return will be reproduced closely in the simulation without making an adjustment. Say you assume asset A has a 5% return and 12% risk. Guess what? Your simulation will have close to a 5% return and 12% risk. Thus we include a noise factor equivalent to a mean of zero and the asset’s standard deviation to account for uncertainty around our estimates.1
Let’s sample four of the return simulations, run the portfolio allocation simulation on them, and graph the output.
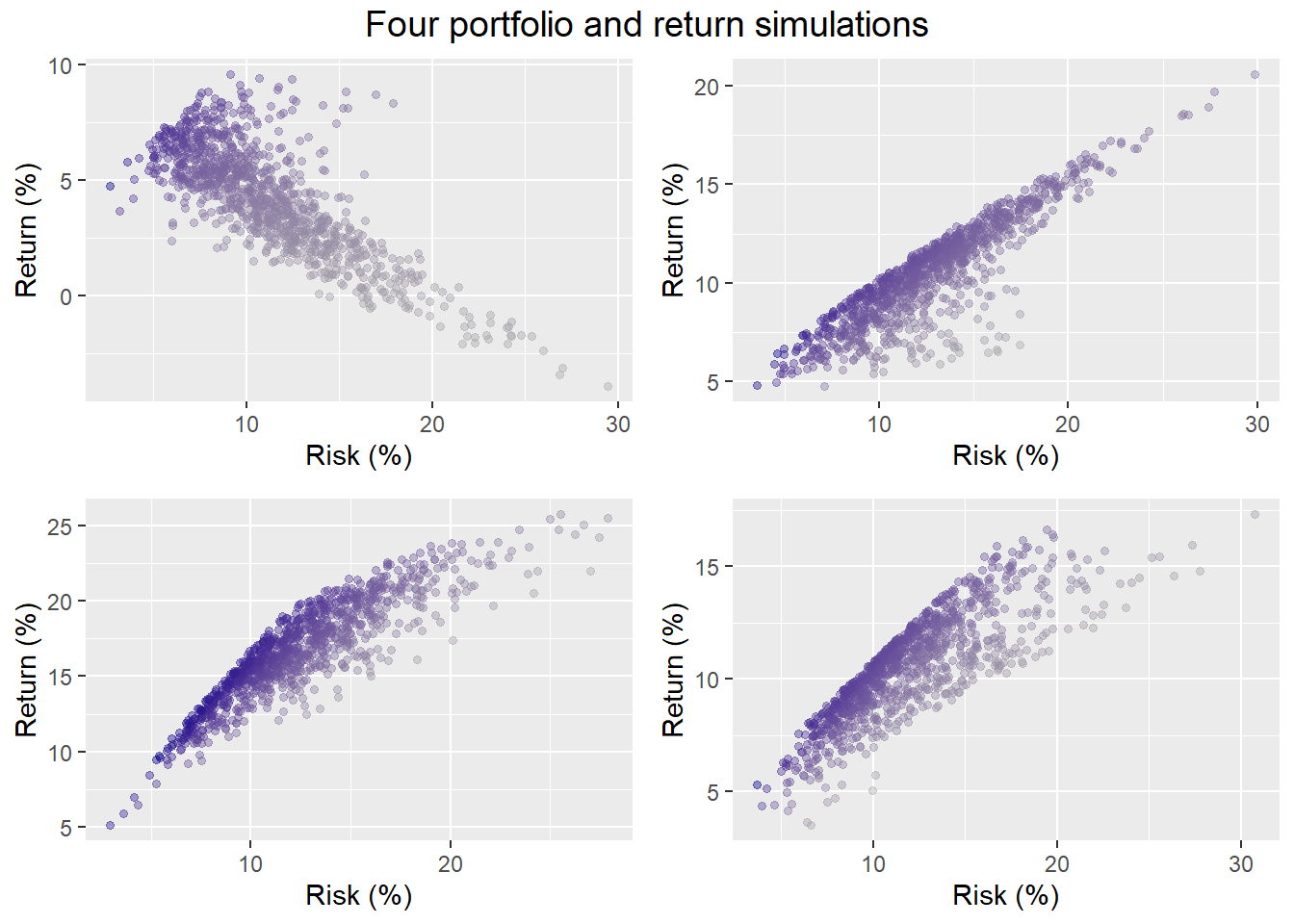
Three of the simulations result in upwardly sloping risk-return portfolios, one does not. Finance theory posits that one should generally be compensated for taking more risk with higher returns. But there are cases where that doesn’t occur. And this isn’t just an artifact of randomness; it happens in reality too. Think of buying stocks before the tech or housing bubbles burst.
Looking in more detail at the graphs, one can see that even if the range of risk is close to the same, returns are not. Hence, the portfolio weights to achieve our risk-return constraints could be quite different, perhaps not even attainable. For example, in three out of four of our samples, just about any allocation would get you returns greater than 7% most of the time. But less than a third of the portfolios would meet the risk constraint. Recall our previous simulation suggested our probability of meeting our risk-return constraints was 27%. Indeed, based on these four samples the likelihood of meeting our risk-return constraints are 8%, 17%, 25%, and 26%. Not a great result.
Second simulation
Critically, these results were only four randomly selected samples from 1,000 simulations. We want to run the portfolio allocation simulation on each of the return simulations. That would yield about a million different portfolios.2
Let’s run these simulations and then graph the histograms. We won’t graph the risk-return scatter plot as we did above for the entire simulation because the results look like a snowstorm in Alaska. Instead, we’ll sample 10,000 portfolios and graph them in the usual way.
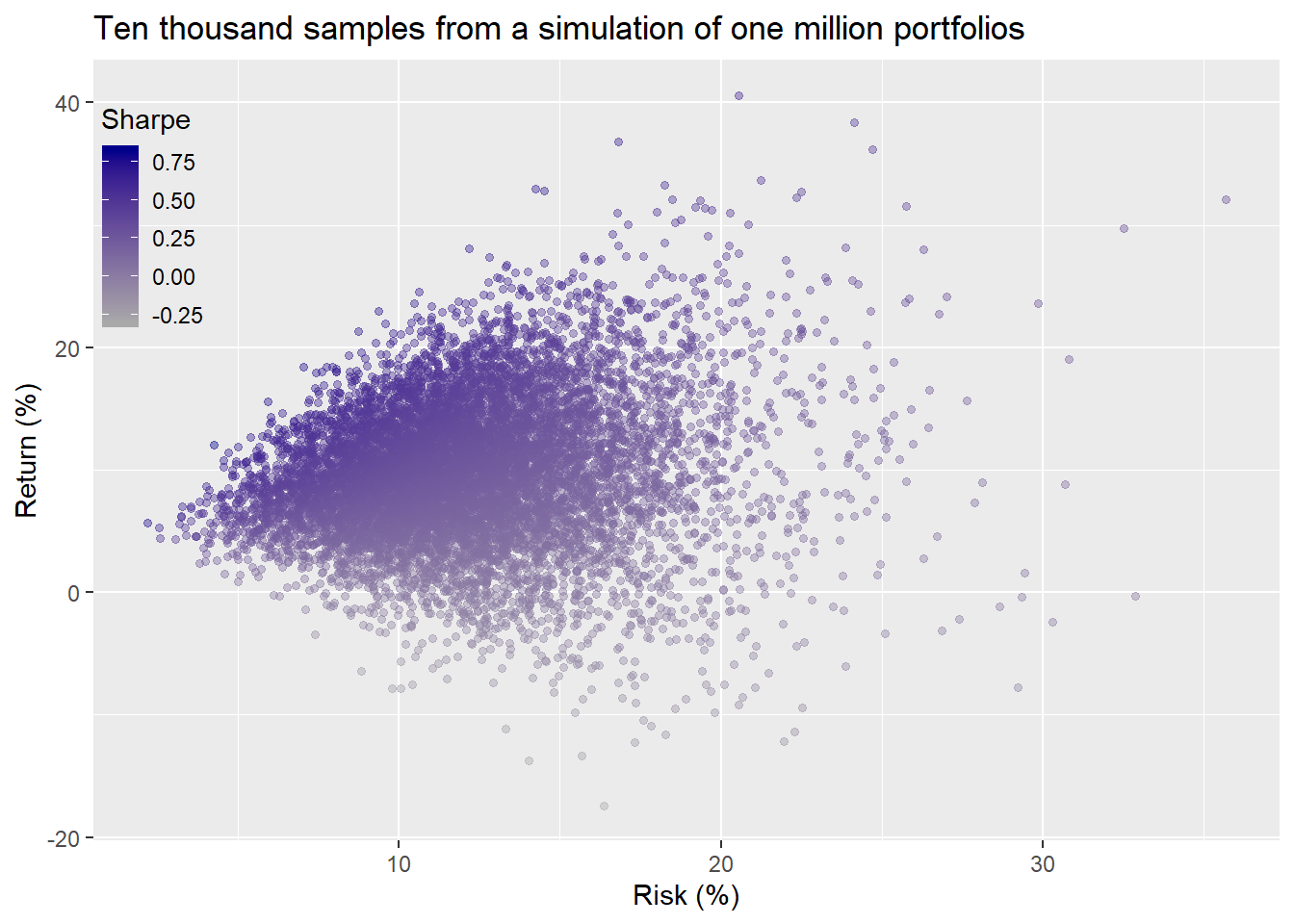
A wide scattering of returns and risk, as one might expect.Here are the return and risk histograms of the million portfolios.
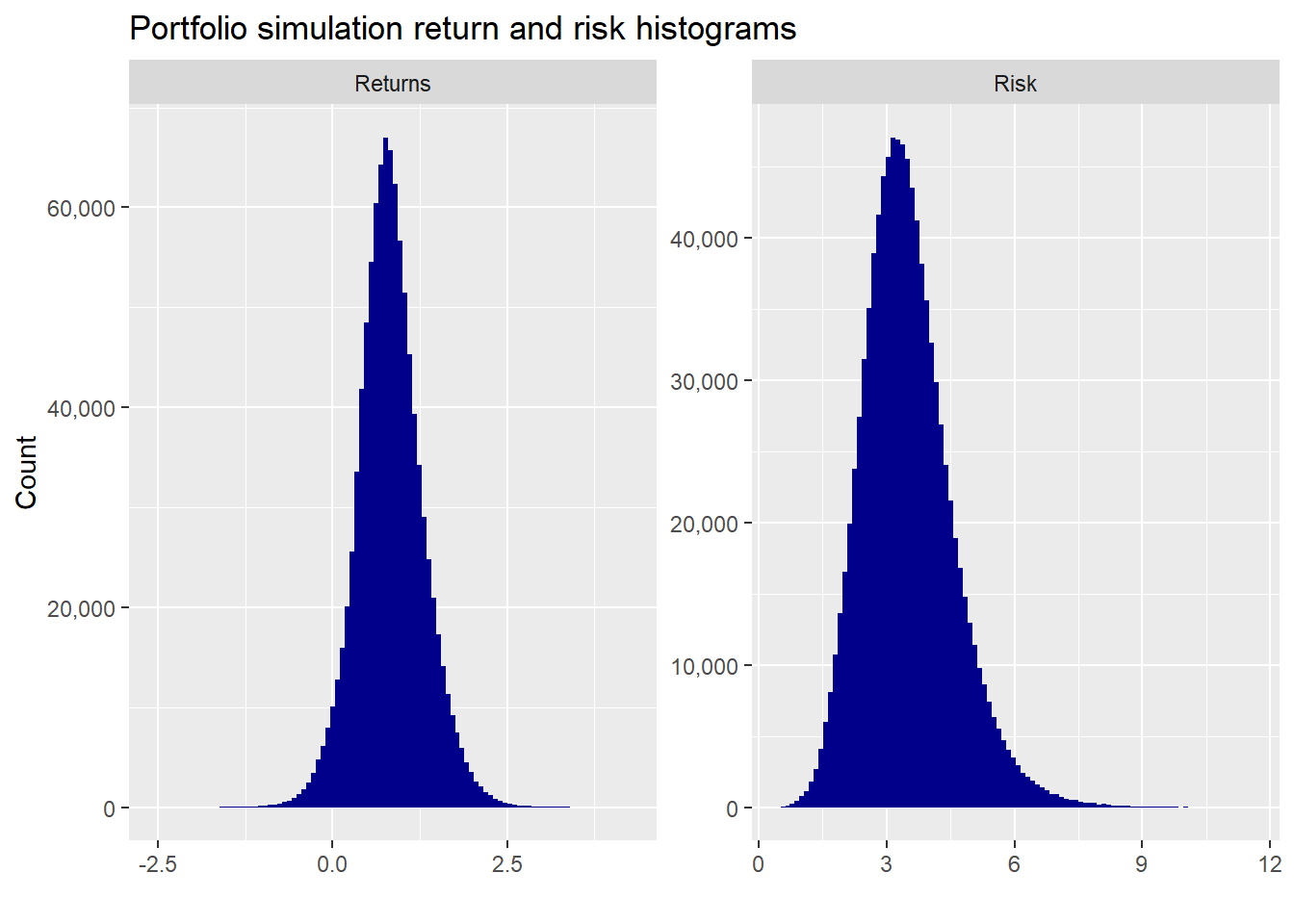
Portfolio returns are close to normally distributed (though that is mostly due to the simulation), while risk is skewed due to the way portfolio volatility is calculated. Suffice it to say, these distributions aren’t unusual. But we should be particularly mindful of the return distribution, which we’ll discuss later.
The average return and risk are 10% and 12% on an annualized basis. That risk level suggests a lower likelihood of hitting our risk- return constraints. Indeed. when we run the calculation, only 19% of the portfolios achieve our goal, lower than our first simulation.
Takeaways
This test offers some solid insights into our original portfolio allocation. First, while our chosen constraints were only achieved in 27% of the portfolios. That didn’t tell us how likely those constraints were to occur over many possible outcomes. Even after the first five-year test, there wasn’t evidence that our constraints were unrealistic because of the time period in which the test fell: namely, the early-to-mid part of the tech boom.
When we ran the second five-year test our portfolio missed our targets. But could we say with confidence that such an outcome was a fluke? It wasn’t until we ran the return and portfolio allocation simulations together that we were able to quantify the likelihood of our targets. As noted, only 19% were likely to meet our constraints. Armed with that knowledge, we should revise our constraints either by lowering our return expectation or increasing our risk tolerance.
If we had run that simulation before our first test, it would have been relatively obvious that the performance was unusual. Indeed, the greater than 9% return with low risk that the portfolio achieved occurred only 14% of the time in our portfolio simulations. The upshot: not impossible, but not all that likely either.
From these results it seems clear that one should be cautious about the period used for a backtest. Clearly, we want to see how the portfolio would have performed historically. But that is only one result from the lab, so to speak.
Critique
While the test results are useful, there are a couple of problems with the analysis we want to point out. First, recall that our portfolio weightings assume we invest some amount in all available assets. If we were to exclude some assets from the portfolio, the range of outcomes would increase, as we showed in our last post. That could increase the probability of meeting our constraints. But we would also want to be careful about how much we should trust that increased probabilty: it’s likely we could get at least a five percentage point improvement simply due to greater randomness.
Second, while we simulated asset returns, we did not simulate correlations, as discussed here. Low correlation among assets reduces portfolio volatility, though variance usually has a bigger impact. But asset correlations are not stable over time. Hence, for completeness our simulations should include the impact of random changes in correlation. We would hope that the random draws implicitly incorporate randomness in correlations, but we’d need to run some calculations to confirm. Alternatively, we could explicitly attempt to randomize the correlations, but that is not as easy as it sounds and can lead to counter-intuitive, or even next to impossible results.3
Third, our simulations drew from a normal distribution and most folks know that returns distributions for financial assets are not normal. One way to solve this is to sample from historical returns. If the sample length and timing were the same across the assets, then we would have partly addressed the correlation issue too. But, as noted before, our data series are not equal in length. Hence, we’d be introducing some bias if we only sampled from those periods in which we had data for every asset.
Fourth, historical returns are not independent of one another. In other words, today’s return on stock ABC, relates, to varying degrees, on ABC’s returns from yesterday or even further out, known as serial correlation. Similarly, ABC’s returns today exhibit some relation to yesterday’s returns for stock DEF, bond, GHI, and so on, known as cross-correlation. Block sampling can address this to a certain degree. But choosing the block size is non-trivial.
Even if we’re able to find a sufficiently long and clean data set, we need to recognize that the returns in that sample, are still that, a sample, and thus not representative of of the full range of possible outcomes (whatever that applies in your cosmology). One need only compare historical returns prior to and after the onset of the covid-19 pandemic to attest to the fact that unexpected return patterns still occur more often than expected in financial data. There a bunch of ways to deal with this including more sophisticated sampling methods, imputing distributions using Bayesian approaches, or bagging exponential smoothing methods using STL decomposition and Box-Cox transformation. We’ll cover the last one in detail in our next post! Kidding aside, we’re a big fan of Prof. Hyndman’s work. But the point is handling unexpected returns requires more and more sophistication. Addressing the merits of adding such sophistication is best left for another post.
Next steps
Let’s review. Over the past seven posts we looked at different methods to set return expectations for assets we might want to include in our portfolio. We then used the simplest method—historical averages—as the foundation for our asset allocation. From there, we simulated a range of possible portfolios, and chose an asset weighting to create a portfolio that would meet our risk-return criteria. We then allocated the assets accordingly and looked at how it performed over two five-year test periods. We noted that rebalancing or exclusion of assets might be warranted, but shelved those temporarily. We then tested how reasonable our risk-return expectations were and found that, in general, they seemed a bit unrealistic. What we haven’t looked at is whether choosing portfolio weights ends up producing a better outcome than the naive equal-weighted portfolio either historically or in simulation. And we also haven’t looked at finding an optimal portfolio for a given level of risk or return. Stay tuned.
Here’s the R followed by the Python code used to produce this post. Order does not reflect preference.
R code:
# Built using R 3.6.2
## Load packages
suppressPackageStartupMessages({
library(tidyquant)
library(tidyverse)
library(grid)
})
## Load data
symbols <- c("WILL5000INDFC", "BAMLCC0A0CMTRIV", "GOLDPMGBD228NLBM", "CSUSHPINSA", "DGS5")
sym_names <- c("stock", "bond", "gold", "realt", "rfr")
getSymbols(symbols, src="FRED", from = "1970-01-01", to = "2019-12-31")
for(i in 1:5){
x <- getSymbols(symbols[i], src = "FRED",
from = "1970-01-01", to = "2019-12-31",
auto.assign = FALSE)
x <- to.monthly(x, indexAt ="lastof", OHLC = FALSE)
assign(sym_names[i],x)
}
dat <- merge(stock, bond, gold, realt, rfr)
colnames(dat) <- sym_names
dat <- dat["1970/2019"]
## create data frame
df <- data.frame(date = index(dat), coredata(dat)) %>%
mutate_at(vars(-c(date, rfr)), function(x) x/lag(x)-1) %>%
mutate(rfr = rfr/100)
df <- df %>% filter(date>="1987-01-01")
## Load simuation function
port_sim <- function(df, sims, cols){
if(ncol(df) != cols){
print("Columns don't match")
break
}
# Create weight matrix
wts <- matrix(nrow = sims, ncol = cols)
for(i in 1:sims){
a <- runif(cols,0,1)
b <- a/sum(a)
wts[i,] <- b
}
# Find returns
mean_ret <- colMeans(df)
# Calculate covariance matrix
cov_mat <- cov(df)
# Calculate random portfolios
port <- matrix(nrow = sims, ncol = 2)
for(i in 1:sims){
port[i,1] <- as.numeric(sum(wts[i,] * mean_ret))
port[i,2] <- as.numeric(sqrt(t(wts[i,]) %*% cov_mat %*% wts[i,]))
}
colnames(port) <- c("returns", "risk")
port <- as.data.frame(port)
port$Sharpe <- port$returns/port$risk*sqrt(12)
max_sharpe <- port[which.max(port$Sharpe),]
graph <- port %>%
ggplot(aes(risk*sqrt(12)*100, returns*1200, color = Sharpe)) +
geom_point(size = 1.2, alpha = 0.4) +
scale_color_gradient(low = "darkgrey", high = "darkblue") +
labs(x = "Risk (%)",
y = "Return (%)",
title = "Simulated portfolios")
out <- list(port = port, graph = graph, max_sharpe = max_sharpe, wts = wts)
}
## Run simuation
set.seed(123)
port_sim_1 <- port_sim(df_old[2:61,2:5],1000,4)
## Load portfolio selection function
port_select_func <- function(port, return_min, risk_max, port_names){
port_select <- cbind(port$port, port$wts)
port_wts <- port_select %>%
mutate(returns = returns*12,
risk = risk*sqrt(12)) %>%
filter(returns >= return_min,
risk <= risk_max) %>%
summarise_at(vars(4:7), mean) %>%
`colnames<-`(port_names)
graph <- port_wts %>%
rename("Stocks" = 1,
"Bonds" = 2,
"Gold" = 3,
"Real estate" = 4) %>%
gather(key,value) %>%
ggplot(aes(reorder(key,value), value*100 )) +
geom_bar(stat='identity', position = "dodge", fill = "blue") +
geom_text(aes(label=round(value,2)*100), vjust = -0.5) +
scale_y_continuous(limits = c(0,40)) +
labs(x="",
y = "Weights (%)",
title = "Average weights for risk-return constraints")
out <- list(port_wts = port_wts, graph = graph)
out
}
## Run selection function
results_1 <- port_select_func(port_sim_1,0.07, 0.1, sym_names[1:4])
## Calculate probability of success
port_success <- round(mean(port_sim_1$port$returns > 0.07/12 &
port_sim_1$port$risk <= 0.1/sqrt(12)),3)*100
## Function for portfolio returns without rebalancing
rebal_func <- function(act_ret, weights){
ret_vec <- c()
wt_mat <- matrix(nrow = nrow(act_ret), ncol = ncol(act_ret))
for(i in 1:60){
wt_ret <- act_ret[i,]*weights # wt'd return
ret <- sum(wt_ret) # total return
ret_vec[i] <- ret
weights <- (weights + wt_ret)/(sum(weights)+ret) # new weight based on change in asset value
wt_mat[i,] <- as.numeric(weights)
}
out <- list(ret_vec = ret_vec, wt_mat = wt_mat)
out
}
## Run function and create actual portfolio and data frame for graph
port_1_act <- rebal_func(df[62:121,2:5],results_1$port_wts)
port_act <- data.frame(returns = mean(port_1_act$ret_vec),
risk = sd(port_1_act$ret_vec),
sharpe = mean(port_1_act$ret_vec)/sd(port_1_act$ret_vec)*sqrt(12))
## Simulate portfolios on first five-year period
set.seed(123)
port_sim_2 <- port_sim(df[62:121,2:5], 1000, 4)
## Graph simulation with chosen portfolio
port_sim_2$graph +
geom_point(data = port_act,
aes(risk*sqrt(12)*100, returns*1200),
size = 4,
color="red") +
theme(legend.position = c(0.05,0.8), legend.key.size = unit(.5, "cm"),
legend.background = element_rect(fill = NA))
## Load longer term data
symbols <- c("WILL5000INDFC", "BAMLCC0A0CMTRIV", "GOLDPMGBD228NLBM", "CSUSHPINSA", "DGS5")
sym_names <- c("stock", "bond", "gold", "realt", "rfr")
for(i in 1:5){
x <- getSymbols(symbols[i], src = "FRED",
from = "1970-01-01", to = "2019-12-31",
auto.assign = FALSE)
x <- to.monthly(x, indexAt ="lastof", OHLC = FALSE)
assign(sym_names[i],x)
}
dat <- merge(stock, bond, gold, realt, rfr)
colnames(dat) <- sym_names
dat <- dat["1970/2019"]
## create data frame
df <- data.frame(date = index(dat), coredata(dat)) %>%
mutate_at(vars(-c(date, rfr)), function(x) x/lag(x)-1) %>%
mutate(rfr = rfr/100)
df <- df %>% filter(date>="1971-01-01")
## Load long data
df <- readRDS('port_const_long.rds')
## Prepare sample
hist_avg <- df %>%
filter(date <= "1991-12-31") %>%
summarise_at(vars(-date), list(mean = function(x) mean(x, na.rm=TRUE),
sd = function(x) sd(x, na.rm = TRUE))) %>%
gather(key, value) %>%
mutate(key = str_remove(key, "_.*"),
key = factor(key, levels =sym_names)) %>%
mutate(calc = c(rep("mean",5), rep("sd",5))) %>%
spread(calc, value)
# Run simulation
set.seed(123)
sim1 <- list()
for(i in 1:1000){
a <- rnorm(60, hist_avg[1,2], hist_avg[1,3]) + rnorm(60, 0, hist_avg[1,3])
b <- rnorm(60, hist_avg[2,2], hist_avg[2,3]) + rnorm(60, 0, hist_avg[2,3])
c <- rnorm(60, hist_avg[3,2], hist_avg[3,3]) + rnorm(60, 0, hist_avg[3,3])
d <- rnorm(60, hist_avg[4,2], hist_avg[4,3]) + rnorm(60, 0, hist_avg[4,3])
df1 <- data.frame(a, b, c, d)
cov_df1 <- cov(df1)
sim1[[i]] <- list(df1, cov_df1)
names(sim1[[i]]) <- c("df", "cov_df")
}
# Sample four return paths
# Note this is the code we used to create the graphs that worked repeatedly when we ran the source code, but would not reproduce accurately in blogdown. Don't know if anyone else has experienced this issue. But after multiple attempts including repasting the code and even seeing the same results when run within the Rmarkdown file, we gave up and read the saved example into blogdown. Let us know if you can't reproduce it.
set.seed(123)
grafs <- list()
for(i in 1:4){
samp <- sample(1000,1)
grafs[[i]] <- port_sim(sim1[[samp]]$df,1000,4)
}
gridExtra::grid.arrange(grafs[[1]]$graph +
theme(legend.position = "none") +
labs(title = NULL),
grafs[[2]]$graph +
theme(legend.position = "none") +
labs(title = NULL),
grafs[[3]]$graph +
theme(legend.position = "none") +
labs(title = NULL),
grafs[[4]]$graph +
theme(legend.position = "none") +
labs(title = NULL),
ncol=2, nrow=2,
top = textGrob("Four portfolio and return simulations",gp=gpar(fontsize=12)))
# Calculate probability of hitting risk-return constraint
probs <- c()
for(i in 1:4){
probs[i] <- round(mean(grafs[[i]]$port$returns >= 0.07/12 &
grafs[[i]]$port$risk <=0.1/sqrt(12)),2)*100
}
probs
## Run simulation
# Portfolio weight function
wt_func <- function(){
a <- runif(4,0,1)
a/sum(a)
}
# Portfolio volatility calculation
vol_calc <- function(cov_dat, weights){
sqrt(t(weights) %*% cov_dat %*% weights)
}
# Simulate
# Note this should run pretty quickly, at least less than a minute.
set.seed(123)
portfolios <- list()
for(i in 1:1000){
wt_mat <- as.matrix(t(replicate(1000, wt_func(), simplify = "matrix")))
avg_ret <- colMeans(sim1[[i]]$df)
returns <- as.vector(avg_ret %*% t(wt_mat))
cov_dat <- cov(sim1[[i]]$df)
risk <- apply(wt_mat, 1, function(x) vol_calc(cov_dat,x))
portfolios[[i]] <- data.frame(returns, risk)
}
port_1m <- do.call("rbind", portfolios)
port_1m_prob <- round(mean(port_1m$returns*12 >= 0.07 & port_1m$risk*sqrt(12) <= 0.1),2)*100
## Graph sample of port_1m
set.seed(123)
port_samp = port_1m[sample(1e6, 1e4),] # choose 10,000 samples from 1,000,000 portfolios.
port_samp %>%
mutate(Sharpe = returns/risk) %>%
ggplot(aes(risk*sqrt(12)*100, returns*1200, color = Sharpe)) +
geom_point(size = 1.2, alpha = 0.4) +
scale_color_gradient(low = "darkgrey", high = "darkblue") +
labs(x = "Risk (%)",
y = "Return (%)",
title = "Ten thousand samples from simulation of one million portfolios") +
theme(legend.position = c(0.05,0.8), legend.key.size = unit(.5, "cm"),
legend.background = element_rect(fill = NA))
# Graph histograms
port_1m %>%
mutate(returns = returns*100,
risk = risk*100) %>%
gather(key, value) %>%
ggplot(aes(value)) +
geom_histogram(bins = 100, fill = "darkblue") +
facet_wrap(~key, scales = "free",
labeller = as_labeller(c(returns = "Returns",
risk = "Risk"))) +
scale_y_continuous(labels = scales::comma) +
labs(x = "",
y = "Count",
title = "Portfolio simulation return and risk histograms")Python code:
# Built using Python 3.7.4
# Load libraries
import pandas as pd
import pandas_datareader.data as web
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
plt.style.use('ggplot')
sns.set()
# Load data
start_date = '1970-01-01'
end_date = '2019-12-31'
symbols = ["WILL5000INDFC", "BAMLCC0A0CMTRIV", "GOLDPMGBD228NLBM", "CSUSHPINSA", "DGS5"]
sym_names = ["stock", "bond", "gold", "realt", 'rfr']
filename = 'data_port_const.pkl'
try:
df = pd.read_pickle(filename)
print('Data loaded')
except FileNotFoundError:
print("File not found")
print("Loading data", 30*"-")
data = web.DataReader(symbols, 'fred', start_date, end_date)
data.columns = sym_names
data_mon = data.resample('M').last()
df = data_mon.pct_change()['1987':'2019']
df.to_pickle(filename) # If you haven't saved the file
df = data_mon.pct_change()['1971':'2019']
pd.to_pickle(df,filename) # if you haven't saved the file
## Simulation function
class Port_sim:
def calc_sim(df, sims, cols):
wts = np.zeros((sims, cols))
for i in range(sims):
a = np.random.uniform(0,1,cols)
b = a/np.sum(a)
wts[i,] = b
mean_ret = df.mean()
port_cov = df.cov()
port = np.zeros((sims, 2))
for i in range(sims):
port[i,0] = np.sum(wts[i,]*mean_ret)
port[i,1] = np.sqrt(np.dot(np.dot(wts[i,].T,port_cov), wts[i,]))
sharpe = port[:,0]/port[:,1]*np.sqrt(12)
best_port = port[np.where(sharpe == max(sharpe))]
max_sharpe = max(sharpe)
return port, wts, best_port, sharpe, max_sharpe
def calc_sim_lv(df, sims, cols):
wts = np.zeros(((cols-1)*sims, cols))
count=0
for i in range(1,cols):
for j in range(sims):
a = np.random.uniform(0,1,(cols-i+1))
b = a/np.sum(a)
c = np.random.choice(np.concatenate((b, np.zeros(i))),cols, replace=False)
wts[count,] = c
count+=1
mean_ret = df.mean()
port_cov = df.cov()
port = np.zeros(((cols-1)*sims, 2))
for i in range(sims):
port[i,0] = np.sum(wts[i,]*mean_ret)
port[i,1] = np.sqrt(np.dot(np.dot(wts[i,].T,port_cov), wts[i,]))
sharpe = port[:,0]/port[:,1]*np.sqrt(12)
best_port = port[np.where(sharpe == max(sharpe))]
max_sharpe = max(sharpe)
return port, wts, best_port, sharpe, max_sharpe
def graph_sim(port, sharpe):
plt.figure(figsize=(14,6))
plt.scatter(port[:,1]*np.sqrt(12)*100, port[:,0]*1200, marker='.', c=sharpe, cmap='Blues')
plt.colorbar(label='Sharpe ratio', orientation = 'vertical', shrink = 0.25)
plt.title('Simulated portfolios', fontsize=20)
plt.xlabel('Risk (%)')
plt.ylabel('Return (%)')
plt.show()
# Plot
np.random.seed(123)
port_sim_1, wts_1, _, sharpe_1, _ = Port_sim.calc_sim(df.iloc[1:60,0:4],1000,4)
Port_sim.graph_sim(port_sim_1, sharpe_1)
## Selection function
# Constraint function
def port_select_func(port, wts, return_min, risk_max):
port_select = pd.DataFrame(np.concatenate((port, wts), axis=1))
port_select.columns = ['returns', 'risk', 1, 2, 3, 4]
port_wts = port_select[(port_select['returns']*12 >= return_min) & (port_select['risk']*np.sqrt(12) <= risk_max)]
port_wts = port_wts.iloc[:,2:6]
port_wts = port_wts.mean(axis=0)
def graph():
plt.figure(figsize=(12,6))
key_names = {1:"Stocks", 2:"Bonds", 3:"Gold", 4:"Real estate"}
lab_names = []
graf_wts = port_wts.sort_values()*100
for i in range(len(graf_wts)):
name = key_names[graf_wts.index[i]]
lab_names.append(name)
plt.bar(lab_names, graf_wts)
plt.ylabel("Weight (%)")
plt.title("Average weights for risk-return constraint", fontsize=15)
for i in range(len(graf_wts)):
plt.annotate(str(round(graf_wts.values[i])), xy=(lab_names[i], graf_wts.values[i]+0.5))
plt.show()
return port_wts, graph()
# Graph
results_1_wts,_ = port_select_func(port_sim_1, wts_1, 0.07, 0.1)
# Return function with no rebalancing
def rebal_func(act_ret, weights):
ret_vec = np.zeros(len(act_ret))
wt_mat = np.zeros((len(act_ret), len(act_ret.columns)))
for i in range(len(act_ret)):
wt_ret = act_ret.iloc[i,:].values*weights
ret = np.sum(wt_ret)
ret_vec[i] = ret
weights = (weights + wt_ret)/(np.sum(weights) + ret)
wt_mat[i,] = weights
return ret_vec, wt_mat
## Run rebalance function using desired weights
port_1_act, wt_mat = rebal_func(df.iloc[61:121,0:4], results_1_wts)
port_act = {'returns': np.mean(port_1_act),
'risk': np.std(port_1_act),
'sharpe': np.mean(port_1_act)/np.std(port_1_act)*np.sqrt(12)}
# Run simulation on first five-year period
np.random.seed(123)
port_sim_2, wts_2, _, sharpe_2, _ = Port_sim.calc_sim(df.iloc[61:121,0:4],1000,4)
# Graph simulation with actual portfolio return
plt.figure(figsize=(14,6))
plt.scatter(port_sim_2[:,1]*np.sqrt(12)*100, port_sim_2[:,0]*1200, marker='.', c=sharpe_2, cmap='Blues')
plt.colorbar(label='Sharpe ratio', orientation = 'vertical', shrink = 0.25)
plt.scatter(port_act['risk']*np.sqrt(12)*100, port_act['returns']*1200, c='red', s=50)
plt.title('Simulated portfolios', fontsize=20)
plt.xlabel('Risk (%)')
plt.ylabel('Return (%)')
plt.show()
# Calculate returns and risk for longer period
# Call prior file for longer period
df = data_mon.pct_change()['1971':'2019']
hist_mu = df['1971':'1991'].mean(axis=0)
hist_sigma = df['1971':'1991'].std(axis=0)
# Run simulation based on historical figures
np.random.seed(123)
sim1 = []
for i in range(1000):
#np.random.normal(mu, sigma, obs)
a = np.random.normal(hist_mu[0], hist_sigma[0], 60) + np.random.normal(0, hist_sigma[0], 60)
b = np.random.normal(hist_mu[1], hist_sigma[1], 60) + np.random.normal(0, hist_sigma[1], 60)
c = np.random.normal(hist_mu[2], hist_sigma[2], 60) + np.random.normal(0, hist_sigma[2], 60)
d = np.random.normal(hist_mu[3], hist_sigma[3], 60) + np.random.normal(0, hist_sigma[3], 60)
df1 = pd.DataFrame(np.array([a, b, c, d]).T)
cov_df1 = df1.cov()
sim1.append([df1, cov_df1])
# create graph objects
np.random.seed(123)
graphs = []
for i in range(4):
samp = np.random.randint(1,1000)
port, _, _, sharpe, _ = Port_sim.calc_sim(sim1[samp][0], 1000, 4)
graf = [port,sharpe]
graphs.append(graf)
# Graph sample portfolios
fig, axes = plt.subplots(2, 2, figsize=(12,6))
for i, ax in enumerate(fig.axes):
ax.scatter(graphs[i][0][:,1]*np.sqrt(12)*100, graphs[i][0][:,0]*1200, marker='.', c=graphs[i][1], cmap='Blues')
plt.show()
# Calculate probability of hitting risk-return constraints based on sample portfolos
probs = []
for i in range(4):
out = round(np.mean((graphs[i][0][:,0] >= 0.07/12) & (graphs[i][0][:,1] <= 0.1/np.sqrt(12))),2)*100
probs.append(out)
# Simulate portfolios from reteurn simulations
def wt_func():
a = np.random.uniform(0,1,4)
return a/np.sum(a)
# Note this should run relatively quickly: less than a minute.
np.random.seed(123)
portfolios = np.zeros((1000, 1000, 2))
for i in range(1000):
wt_mat = np.array([wt_func() for _ in range(1000)])
port_ret = sim1[i][0].mean(axis=0)
cov_dat = sim1[i][0].cov()
returns = np.dot(wt_mat, port_ret)
risk = [np.sqrt(np.dot(np.dot(wt.T,cov_dat), wt)) for wt in wt_mat]
portfolios[i][:,0] = returns
portfolios[i][:,1] = risk
port_1m = portfolios.reshape((1000000,2))
# Find probability of hitting risk-return constraints on simulated portfolios
port_1m_prob = round(np.mean((port_1m[:][:,0] > 0.07/12) & (port_1m[:][:,1] <= 0.1/np.sqrt(12))),2)*100
print(f"The probability of meeting our portfolio constraints is:{port_1m_prob: 0.0f}%")
# Plot sample portfolios
np.random.seed(123)
port_samp = port_1m[np.random.choice(1000000, 10000),:]
sharpe = port_samp[:,0]/port_samp[:,1]
plt.figure(figsize=(14,6))
plt.scatter(port_samp[:,1]*np.sqrt(12)*100, port_samp[:,0]*1200, marker='.', c=sharpe, cmap='Blues')
plt.colorbar(label='Sharpe ratio', orientation = 'vertical', shrink = 0.25)
plt.title('Ten thousand samples from one million simulated portfolios', fontsize=20)
plt.xlabel('Risk (%)')
plt.ylabel('Return (%)')
plt.show()
# Graph histograms
fig, axes = plt.subplots(1,2, figsize = (12,6))
for idx,ax in enumerate(fig.axes):
if idx == 1:
ax.hist(port_1m[:][:,1], bins = 100)
else:
ax.hist(port_1m[:][:,0], bins = 100)
plt.show()Since we’re using monthly returns, it should be obvious why our noise isn’t N[0,1]. Nonetheless, our approach seems more art than science. If you know a better method to add noise to such simulations, please email us at the address below.↩
When we first started learning R, we kept reading why one should avoid for loops. We didn’t really get what the big issue was. That is until now. Of course, at the time, we could barely wrap our heads around a for loop in the first place. When we tried to run the 1,000 return simulations for 1,000 portfolios each, our poor old laptop was still cycling after 20 minutes. After we moved the calculations into some apply functions (which we still don’t always understand, either), it finished in under 10 minutes. When we vectorized some of the functions except for the volatility calculation we got it down to under a minute. The python code went in a similar fashion except there isn’t a python version of apply(). There is an apply “method” for pandas data frames. Confusing right? Nevertheless, using the apply method on a pandas data frame made things worse. Putting most everything into numpy, as suggested by a gracious reader, except for one list comprehension did the trick. No doubt we could improve performance further, but aren’t sure how at this stage. If you have any suggestions, please email us. We’d really appreciate it!↩
See this discussion for more detail.↩