Statistically speaking
In our last post, we defined the goal of an investment strategy, showed how comparing strategies may not be as straightforward as one would imagine, and outlined some critical questions that need to be answered when weighing competing strategies. In this post, we’ll look at what an investment strategy’s main constraints — namely, return and risk — actually imply.
What do the numbers say?
Assume you’ve chosen the strategy and assume it’s simple: invest in a large index of stocks, namely the S&P500. Assume your required return is 7% (the S&P is close to that over the long term) and you don’t want to see annual results vary up or down by more than 16% from that average (also close to the S&P annual volatility). What would that look like? Let’s simulate nine stock indices that feature such constraints and graph the cumulative return path over a 20-year period.
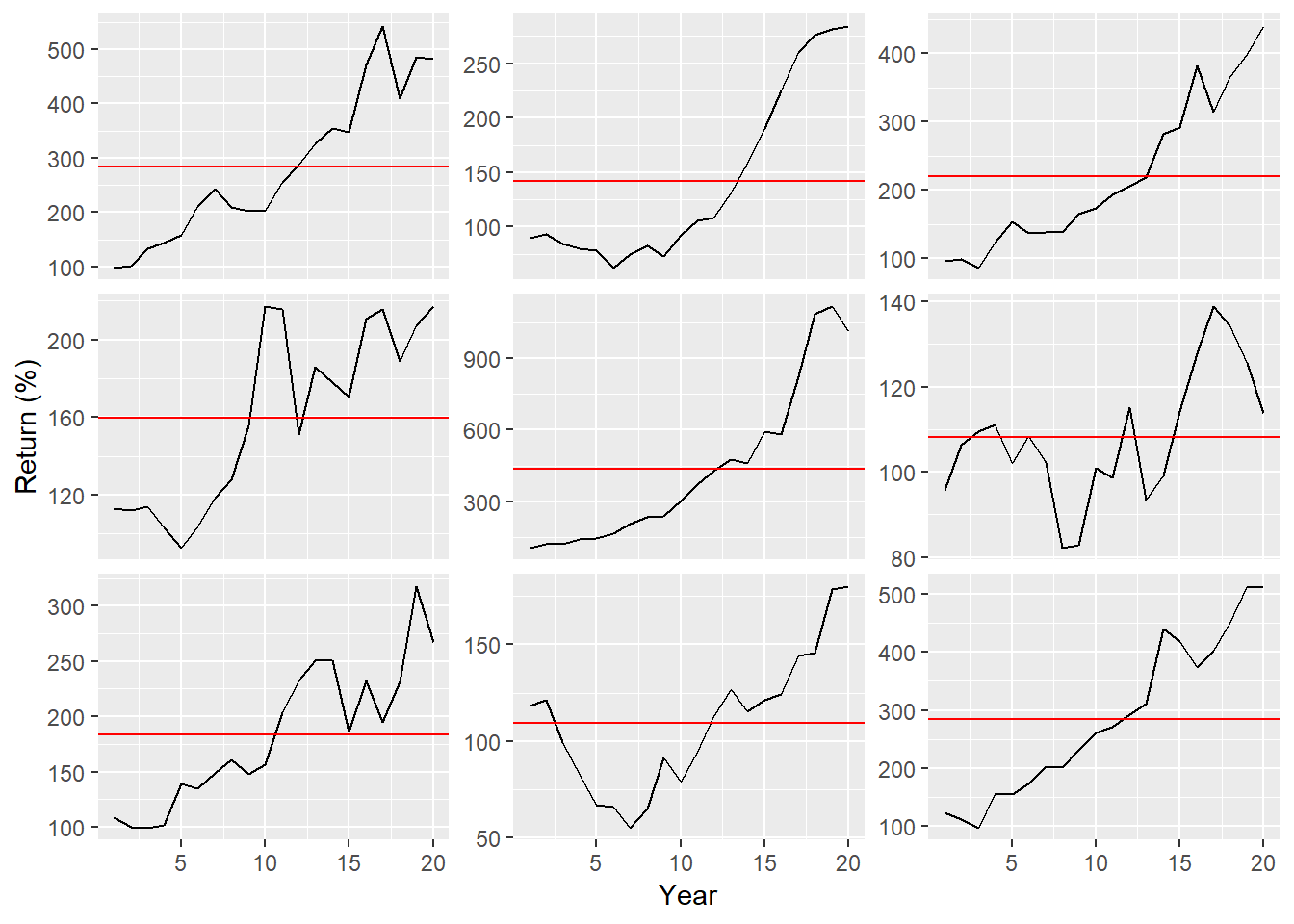
While all the stocks appear to be upwardly trending, we adjusted the scale to see each path more clearly. If we put those results into a table, showing the total return and annual deviation, we see how variable the end result can be. Recall, we established a required return of about 7% a year, which equates to almost a 300% return at the end of twenty years. Only four out of the nine examples made the cut-off. Two severely missed the mark.
| Index | Total return (%) | Risk (%) |
|---|---|---|
| A | 382.0 | 15.6 |
| B | 184.6 | 13.3 |
| C | 340.1 | 15.3 |
| D | 117.3 | 15.6 |
| E | 912.7 | 13.3 |
| F | 13.8 | 11.2 |
| G | 166.8 | 17.4 |
| H | 80.2 | 16.5 |
| I | 412.1 | 17.2 |
Of course, this example is only a small subset of possible outcomes. Assuming we’re right about the expected return and variability (a big assumption!), over a large range of possible results the average return would tend toward 7% annually yielding a cumulative return of that required 300%. But what are the range of possible outcomes around that average?
We run 100,000 simulations of the risk and return parameters described above and then graph those simulations, showing the average cumulative return (red line) and reasonable boundaries of those returns (blue lines). The blue bounds are the range of results we would expect to see 70% of the time. We cut the graph above 1000% to make it more readable.
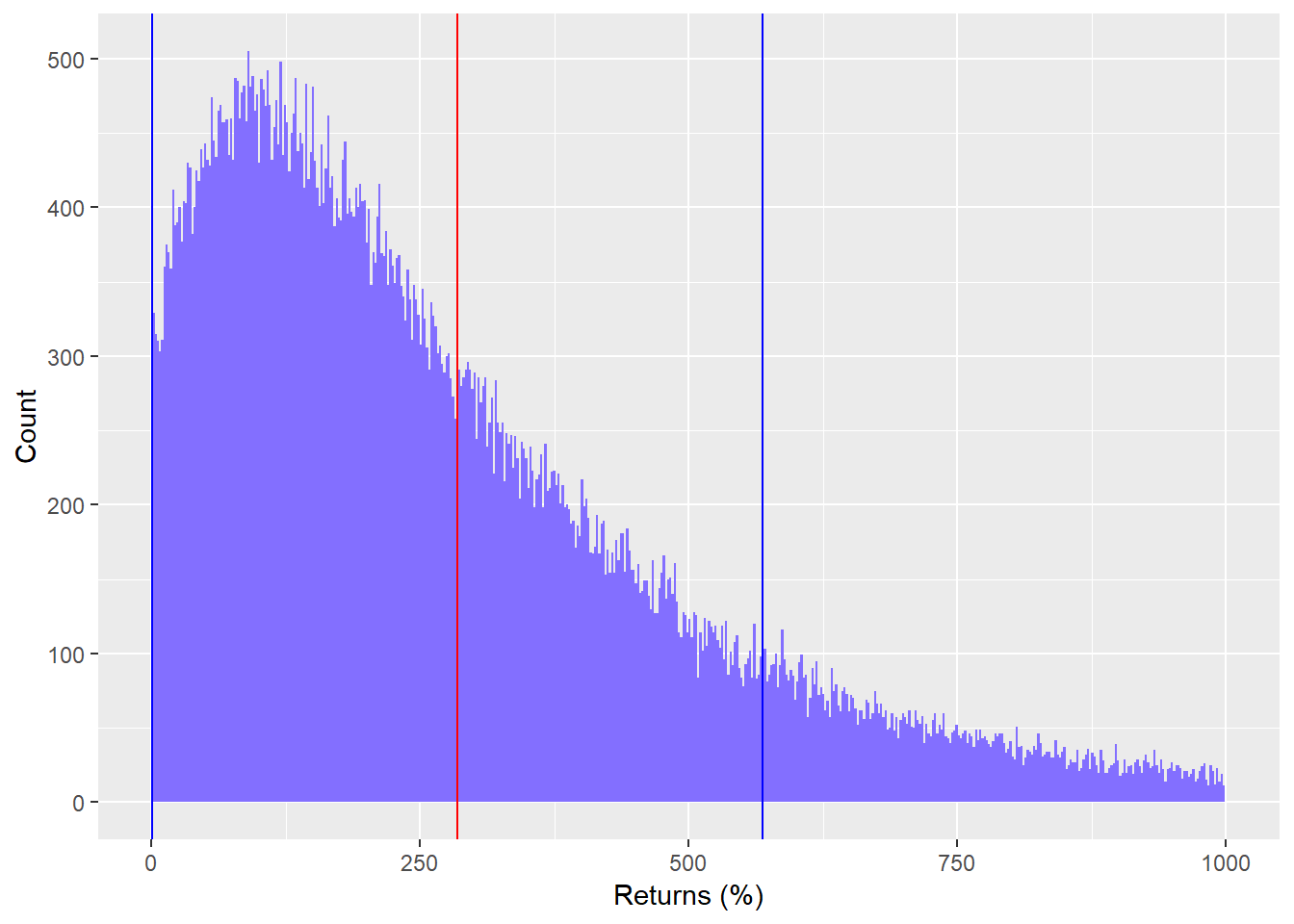
You might think, “Great! Looks like there’s plenty of room to hit my target.” But there’s a problem here. Everyone has only one chance of hitting his or her target, not 100,000 chances! How do you account for the risk that your chosen strategy fails? One way is to establish a threshold which you wouldn’t want the strategy to exceed and then calculate how likely that threshold might be breached. For example, we might state that although our required return is 7% per year, equating to a 290% cumulative return, we cannot tolerate a cumulative return of less than 230%. Seems pretty conservative, right? we’re willing to accept a cumulative return 60 percentage points below average. Let’s forget for a moment how we came up with that threshold.
What’s the likelihood of that happening based on these simulations? 54%! It would be crazy to leave your investment goals up to a coin toss.
Even if we were to lower the threshold to a 200% cumulative return, there’s still a 48% chance results would be worse than that. This is one of the main problems with folks that trot out recommendations of investing for the long term and support those recommendations with graphs based on 200 years of data. It confuses lots of data with lots of occurrences. History is just one pick from the marble jar of infinite occurrences! And that’s what those graphs and data represent — one marble.
What do you do to offset the risk of completing missing your investment goal? On first glance, if you only have two constraints — risk and return — then you have to play with those to lower shortfall risk. We’ll look at some of those trade-offs in another post to see how much wiggle room one might have.
Diversifying across strategies that don’t correlate well with one another is another method. Note, in this post we only looked at one strategy, which is a bit simplistic relative to how most portfolios are constructed. But diversification adds complexity by adding a third estimate — correlation. More on that in another post.
A third way is to apply some tactical constraints on how to execute the strategy. For example, only invest in an asset if it is above or confirms some pre-determined threshold or trend. Implementing such a tactic opens a debate on market timing, which is a can of worms best left closed for now. Still, we’ll investigate some tactical strategies that appear to persist, which could prove interesting. But that again is for another post. Until next time.
Here is the code behind everything above:
# Load package
library(tidyquant)
# Create dataset
set.seed(123)
stocks <- matrix(nrow = 20, ncol =9)
for(i in 1:9){
stocks[,i] <- rnorm(20, 0.07, 0.16)
}
stocks <- data.frame(year = 1:20, stocks)
colnames(stocks)[-1] <- toupper(letters[1:9])
stocks <- stocks %>% gather(stock, return, -year)
# Graph data
stocks %>%
group_by(stock) %>%
mutate(return = cumprod(return + 1),
avg = mean(return, na.rm = TRUE)) %>%
ggplot(aes(year, return*100)) +
geom_line() +
geom_hline(aes(yintercept = avg*100), color = "red") +
xlab("Year") + ylab("Return (%)") +
facet_wrap(.~stock, scales = "free_y") +
theme(strip.background = element_blank(),
strip.text.x = element_blank())
# Table
stocks %>%
group_by(stock) %>%
summarise(total = round(Return.cumulative(return),3)*100,
risk = round(sd(return),3)*100) %>%
rename("Stock" = stock,
"Total return (%)" = total,
"Risk (%)" = risk) %>%
knitr::kable()
# Return function
return_func <- function(years, return, risk){
stock <- rnorm(years, return, risk)
cum_ret <- Return.cumulative(stock)
return(cum_ret)
}
# Repleicate 100000 samples
set.seed(123)
out <- replicate(100000, return_func(20, 0.07, 0.16))
out <- out*100
out <- out %>% data.frame()
names(out) <- "returns"
# Graph histogram
out %>%
ggplot(aes(returns)) +
geom_histogram(bins = 500, fill = "slateblue1") +
xlim(c(0,1000))+
xlab("Returns (%)") + ylab("Count") +
geom_vline(xintercept = mean(out$returns), color = "red") +
geom_vline(xintercept = mean(out$returns) + sd(out$returns), color = "blue") +
geom_vline(xintercept = mean(out$returns) - sd(out$returns), color = "blue")